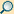Bohr-sommerfeldsches Atommodell
Das bohr-sommerfeldsche Atommodell, sommerfeldsche Atommodell oder die Sommerfeld-Erweiterung ist eine physikalische Beschreibung der Elektronenbahnen in einem Atom. Es wurde 1915/16 von Arnold Sommerfeld vorgeschlagen und stellt eine Verfeinerung des bohrschen Atommodells dar.
Überblick
Das bohr-sommerfeldsche Atommodell von 1916 baut auf dem bohrschen Modell von 1913 auf und ist damit eine der älteren Quantentheorien vor Entwicklung der Quantenmechanik. Es wird angenommen, dass sich die Elektronen um den Atomkern auf wohldefinierten Bahnen bewegen, die sich aus den Bewegungsgleichungen zunächst der klassischen Mechanik ergeben, also auf den aus der Planetenbewegung bekannten Ellipsen. Quantentheoretische Prinzipien werden durch zusätzliche Quantisierungsbedingungen (Bohr-Sommerfeld-Quantisierung) eingeführt. Diese führen dazu, dass nur eine kleine Auswahl der Bahnen erlaubt ist, die nach der klassischen Mechanik möglich wären. Als Folge davon können auch die mit der Bahnbewegung verbundenen Erhaltungsgrößen (Energie und Drehimpuls) nicht mehr beliebige, sondern nur noch bestimmte, diskrete Werte annehmen, sie sind also „gequantelt“.
Der Fortschritt des sommerfeldschen Atommodells gegenüber seinem Vorgänger besteht vor allem darin, dass es die Feinstruktur des Wasserstoffspektrums, d.h. die kleinen Aufspaltungen der klassisch berechneten Energien, berechenbar macht (Feinstrukturkonstante), indem es die Bewegungsgleichung der speziellen Relativitätstheorie berücksichtigt. Die Feinstruktur wird mit der Erhöhung der trägen Masse begründet, welche die spezielle Relativitätstheorie für steigende Geschwindigkeit voraussagt. Bei gleicher Hauptquantenzahl n ist dieser Effekt umso stärker, je näher das Elektron im Perihel am Kern vorbeifliegt, je größer also die numerische Exzentrizität der Ellipse bzw. je kleiner der Bahndrehimpuls ist. Die unterschiedlichen Bahnen zu einer Hauptquantenzahl haben nicht mehr exakt das gleiche Energieniveau, sondern die Energie wird auch vom Bahndrehimpuls abhängig.
Ein weiterer Fortschritt des sommerfeldschen Atommodells ist, dass es den normalen Zeeman-Effekt und den Stark-Effekt erklären kann.
Das bohr-sommerfeldsche Atommodell hat wegen seiner Anschaulichkeit hohen Erklärungswert; statt der bisher im bohrschen Modell begründeten einzigen Quantenzahl der Elektronenzustände lieferte es richtig alle drei räumlichen Quantenzahlen und ermöglichte damit erstmals eine wenigstens qualitative physikalische Erklärung des Periodensystems der chemischen Elemente.
Das bohr-sommerfeldsche Modell versagt aber wie schon das bohrsche Modell bei allen Berechnungen von Atomen mit mehr als einem Elektron. Dass dieser Fehlschlag von der irrigen Annahme definierter, klassischer Teilchenbahnen herrührte, wurde ab 1925 deutlich, als die neue Quantenmechanik wesentlich mehr Beobachtungen erklären und Vorhersagen machen konnte, und diese sogar zumeist quantitativ richtig. In ihr gibt es keine definierten Bahnen mehr, wie man z.B. an der heisenbergschen Unschärferelation erkennen kann, sondern nur noch Wahrscheinlichkeitsverteilungen.
Geometrie der Elektronenbahnen
Während im Modell von Niels Bohr die möglichen Bahnen des Elektrons Kreise um den Atomkern sind, führte Sommerfeld allgemeinere Ellipsenbahnen ein, als deren Spezialfall der Kreis noch vorkommt. Der Kern befindet sich nach diesem Modell in einem der beiden Brennpunkte einer Bahnellipse, so dass sich eine geometrische Konfiguration wie bei den Planetenbahnen nach den keplerschen Gesetzen ergibt. Auf diesen Bahnen soll sich – wie im bohrschen Modell – das Elektron ohne Emission elektromagnetischer Strahlung bewegen, wie sie nach der klassischen Elektrodynamik auftreten müsste.
Das bohr-sommerfeldsche Modell stellt also ein keplersches Planetensystem im Kleinen dar, während das bohrsche Modell der älteren kopernikanischen Vorstellung entspricht. Diese Analogie ist naheliegend, da die Kraftfelder der Coulombkraft des Atomkerns und der Gravitation der Sonne die gleiche Form haben:
Die Berücksichtigung der speziellen Relativitätstheorie ergibt Bahnen näherungsweise in Form einer Ellipse, deren Hauptachse sich langsam dreht (Periheldrehung).
Bohr-Sommerfeld-Quantisierung
Eine Ellipse kann nicht mehr wie ein Kreis durch einen einzigen Parameter
(Radius) beschrieben werden, vielmehr benötigt man dazu zwei (z.B. große
und kleine Halbachse).
Deshalb sind bei Ellipsenbahnen zwei Quantenzahlen notwendig, um die Form
festzulegen. Eine dritte benötigt man für die Orientierung der Bahnebene im Raum. Eine
Quantenzahl davon, aber auch nur eine, kann die bohrsche Quantisierung der
Kreisbewegung beisteuern, denn im kugelsymmetrischen Potential des
Atomkerns besitzen alle Bahnen einen bestimmten Drehimpuls.
Sommerfeld verallgemeinerte Bohrs Quantisierung dahingehend, dass jede
Koordinate
eine eigene Quantenbedingung erfüllen muss:
Darin ist
eine Koordinate
ihr kanonisch zugeordneter Impuls
die Quantenzahl
das plancksche Wirkungsquantum.
Das Kurvenintegral
ist die Fläche innerhalb der betreffenden Bahn in der -Ebene.
Es wird in der Mechanik als die Wirkung
bezeichnet, die dieser Bewegung zugeordnet ist.
Im 1-dimensionalen Fall kann
einfach die x-Koordinate und
der gewöhnliche Impuls sein. Dann ergibt sich
aus der Quantenbedingung z.B. sofort die Quantisierung des harmonischen
Oszillators mit Energiestufen
.
Durch kanonische
Transformation kann man jedoch zu anderen Variablen kommen, die dann
automatisch die gleiche Bedingung erfüllen.
Bei Bewegung in zwei oder drei Dimensionen kann man als Koordinate z.B.
einen Drehwinkel
wählen, wozu als kanonischer Impuls dann der Drehimpuls
gehört. Das Wirkungsintegral für einen vollen Umlauf ist dann
und es ergibt sich die Drehimpulsquantisierung wie bei Bohr zu
Quantenzahlen
Sommerfeld betrachtet das System in den drei Kugelkoordinaten
(Abstand r und zwei Winkel) und unterwirft jede der neuen
Quantisierungsbedingung. So erhält er drei Quantenzahlen: die radiale
,
die azimutale
und die magnetische
.
Hauptquantenzahl
Die Quantenzahl n, die wie im bohrschen Modell und in den Rydberg-Formeln auch hier die Energie bestimmt, wird nun Hauptquantenzahl genannt und erweist sich als
bzw. eigentlich als
Nebenquantenzahl
Die azimutale Quantenzahl ,
nun Nebenquantenzahl genannt, gibt den (Bahn-)Drehimpuls
an (
ist die plancksche
Konstante
geteilt durch
.)
Bei gegebenem n kann die Nebenquantenzahl als Werte die natürlichen Zahlen
von 1 bis
annehmen:
wobei der größtmögliche Drehimpuls ()
zur bohrschen Kreisbahn gehört. Ausdrücklich wird der Wert
ausgeschlossen, weil in diesem Fall das Elektron auf einer Geraden hin und her
schwingt, die durch den Kern geht.
_kl.png)
Nach der quantenmechanischen
Berechnung, die ab 1925 das Bohr-Sommerfeld-Modell ablöste, ist der
Drehimpuls allerdings um genau eine Einheit
geringer und der richtige Wertebereich folglich
(s. auch nebenstehende Abb.). Zu
gehört dabei ein kugelsymmetrisches Orbital.
Magnetische Quantenzahl
Die magnetische Quantenzahl
gibt den Neigungswinkel
des Drehimpulses
gegen die z-Achse an, bzw. genau genommen die Größe der Projektion
des Drehimpulses
auf die z-Achse:
Der Wertebereich dieser Quantenzahl ist
insgesamt
verschiedene Werte. Damit ist die Richtungsquantelung
vorhergesagt, denn es gibt von genau parallel zu genau antiparallel nur diese
endliche Anzahl von Einstellmöglichkeiten. (Die Quantenmechanik gibt dem
Drehimpulsvektor statt
die Länge
wodurch die beiden extremen Einstellmöglichkeiten
doch nicht ganz mit der z-Achse zusammenfallen.)
Das sich um den Atomkern bewegende Elektron bildet einen magnetischen Dipol
,
dessen Richtung senkrecht auf der Bahnellipse steht, also parallel zum Vektor
des Bahndrehimpulses. Bringt man das Atom in ein äußeres Magnetfeld
(das die z-Achse definiert), dann hängt seine Energie auch vom Einstellwinkel
ab. Wegen der Richtungsquantelung spaltet die Energie je nach dem Wert der
magnetischen Quantenzahl (daher ihr Name) in
verschiedene Werte auf (Zeeman-Effekt).
Spinquantenzahl
Neben diesen im bohr-sommerfeldschen Atommodell eingeführten
räumlichen Quantenzahlen gibt es für jedes Elektron auch noch die
Spinquantenzahl
für die stets genau zwei Einstellmöglichkeiten seines Eigendrehimpulses (Spin). Sie wird mit
den Werten +½ oder −½ beziehungsweise den Symbolen ↑ oder ↓ angegeben. Diese
Quantenzahl resultiert nicht aus Sommerfelds Quantisierungsbedingungen, sondern
wurde später aufgrund sonst unerklärlicher experimenteller Befunde (z.B.
geradzahlige Aufspaltung im Stern-Gerlach-Versuch
und im anomalen Zeeman-Effekt)
ins Modell eingefügt. Die Energie jeder der bisher genannten Bahnen kann dadurch
in zwei Energien aufgespalten werden.
Pauli-Verbot
Aufgrund der durch das sommerfeldsche Modell ermöglichten Ordnung im Verständnis des Atomaufbaus konnte Wolfgang Pauli 1925 das Pauli-Verbot entdecken: Jede der durch die drei räumlichen Quantenzahlen bestimmten Bahn kann maximal zwei Elektronen aufnehmen, die dann entgegengesetzte Spinquantenzahl haben müssen.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 14.08. 2023