Normalenform

Die Normalenform, Normalform oder Normalengleichung ist in der Mathematik eine spezielle Form einer Geradengleichung oder Ebenengleichung. In der Normalenform wird eine Gerade in der euklidischen Ebene oder eine Ebene im euklidischen Raum durch einen Stützvektor und einen Normalenvektor dargestellt. Eine Gerade oder Ebene besteht dann aus denjenigen Punkten in der Ebene oder im Raum, für die der Differenzvektor aus Ortsvektor und Stützvektor senkrecht zum Normalenvektor steht. Die Normalenform ist damit eine spezielle implizite Darstellung der Gerade oder Ebene.

Eine Variante der Normalenform stellt die hessesche Normalform dar, bei der der Normalenvektor normiert und orientiert ist und statt des Stützvektors der Abstand vom Koordinatenursprung verwendet wird.

Normalenform einer Geradengleichung

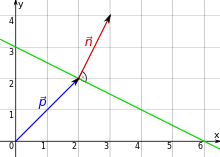
Normalenform der Geradengleichung $x+2y-6=0$

Darstellung

In der Normalenform wird eine Gerade in der Ebene durch einen Stützvektor ${\vec {p}}$ und einen Normalenvektor ${\vec {n}}$ beschrieben. Eine Gerade besteht dann aus denjenigen Punkten in der Ebene, deren Ortsvektoren ${\vec {x}}$ die Gleichung

$({\vec {x}}-{\vec {p}})\cdot {\vec {n}}=0$

erfüllen. Hierbei bezeichnet $\cdot$ das Skalarprodukt zweier Vektoren, welches null ist, wenn die Vektoren senkrecht aufeinander stehen. Der Stützvektor ist der Ortsvektor eines beliebigen Punkts auf der Gerade, der auch als Stützpunkt oder Aufpunkt bezeichnet wird. Der Normalenvektor ist ein Vektor, der mit der Gerade einen rechten Winkel bildet. In der Normalenform werden demnach die Punkte der Geraden implizit dadurch definiert, dass der Differenzvektor aus Ortsvektor und Stützvektor senkrecht zum Normalenvektor der Gerade steht. Eine äquivalente Darstellung der Normalenform ist

${\vec {x}}\cdot {\vec {n}}={\vec {p}}\cdot {\vec {n}}$ .

Ein Punkt, dessen Ortsvektor ${\vec {x}}$ die Normalengleichung nicht erfüllt, liegt für ${\vec {x}}\cdot {\vec {n}}>{\vec {p}}\cdot {\vec {n}}$ auf derjenigen Seite der Gerade, in die der Normalenvektor zeigt, und ansonsten auf der anderen Seite.

Beispiel

Ausgeschrieben lautet die Normalenform einer Geradengleichung

$(x_{1}-p_{1})\cdot n_{1}+(x_{2}-p_{2})\cdot n_{2}=0$ .

Im Bild oben ist beispielsweise der Stützvektor ${\vec {p}}={\tbinom {2}{2}}$ und der Normalenvektor ${\vec {n}}={\tbinom {1}{2}}$ , und man erhält als Geradengleichung

$(x_{1}-2)\cdot 1+(x_{2}-2)\cdot 2=0$ .

Jede Wahl von $(x_{1},x_{2})$ , die diese Gleichung erfüllt, beispielsweise (2,2) oder (4,1) , entspricht dann einem Geradenpunkt.

Berechnung

Aus der Parameterform

Aus der Parameterform einer Geradengleichung lässt sich ein Normalenvektor der Geraden bestimmen, indem die beiden Komponenten des Richtungsvektors ${\vec {u}}$ der Geraden vertauscht werden und bei einer der beiden Komponenten das Vorzeichen geändert wird, das heißt

${\vec {n}}={\begin{pmatrix}-u_{2}\\u_{1}\end{pmatrix}}$ .

Der Stützvektor ${\vec {p}}$ kann aus der Parameterform übernommen werden.

Aus der Zweipunkteform

Aus der Zweipunkteform einer Geradengleichung wird zunächst ein Richtungsvektor der Geraden als Differenzvektor zwischen den Ortsvektoren ${\vec {p}}$ und ${\vec {q}}$ der beiden Punkte ermittelt und dann wie bei der Parameterform verfahren, also

${\vec {n}}={\begin{pmatrix}-(q_{2}-p_{2})\\q_{1}-p_{1}\end{pmatrix}}$ .

Als Stützvektor ${\vec {p}}$ kann der Ortsvektor einer der Punkte verwendet werden.

Aus der Koordinatenform

Aus der Koordinatenform einer Geradengleichung mit den Parametern a,b und lässt sich ein Normalenvektor der Gerade direkt als

${\vec {n}}={\begin{pmatrix}a\\b\end{pmatrix}}$

ablesen. Einen Stützvektor der Gerade erhält man, je nachdem ob oder ungleich null ist, durch Wahl von

${\vec {p}}={\begin{pmatrix}c/a\\0\end{pmatrix}}$ oder ${\vec {p}}={\begin{pmatrix}0\\c/b\end{pmatrix}}$ .

Analog lässt sich auf diese Weise auch aus der Achsenabschnittsform einer Geradengleichung ein Normalenvektor und ein Stützvektor ermitteln.

Normalenform einer Ebenengleichung

Normalenform einer Ebenengleichung

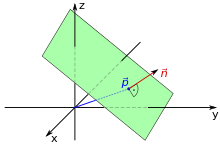
Darstellung

Analog wird eine Ebene im dreidimensionalen Raum in der Normalenform ebenfalls durch einen Stützvektor ${\vec {p}}$ und einen Normalenvektor ${\vec {n}}$ beschrieben. Eine Ebene besteht dann aus denjenigen Punkten im Raum, deren Ortsvektoren ${\vec {x}}$ die Gleichung

$({\vec {x}}-{\vec {p}})\cdot {\vec {n}}=0$

erfüllen. Der Stützvektor ist dabei wiederum der Ortsvektor eines beliebigen Punkts in der Ebene und der Normalenvektor ist ein Vektor, der senkrecht auf der Ebene steht. Das bedeutet, dass der Normalenvektor mit allen Geraden der Ebene, die durch den Stützpunkt verlaufen, einen rechten Winkel bildet. Eine äquivalente Darstellung der Normalenform ist wiederum

${\vec {x}}\cdot {\vec {n}}={\vec {p}}\cdot {\vec {n}}$

und ein Punkt, dessen Ortsvektor ${\vec {x}}$ die Normalengleichung erfüllt, liegt auf der Ebene. Gilt ${\vec {x}}\cdot {\vec {n}}>{\vec {p}}\cdot {\vec {n}}$ , dann liegt der Punkt auf derjenigen Seite der Ebene, in die der Normalenvektor zeigt, ansonsten auf der anderen Seite.

Beispiel

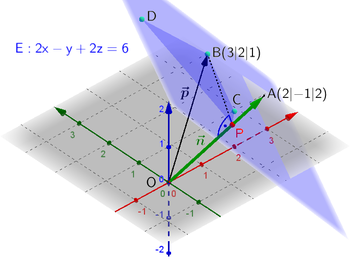
Die Ebene (blau) verläuft rechtwinklig zur Strecke $\overline{OA}$ (grün) durch denn Punkt (rot). Auf derselben Ebene liegen auch die Punkte (türkis) $B(3,2,1)$ , $C(2,0,1)$ und $D(1,2,3)$

Ausgeschrieben lautet die Normalenform einer Ebenengleichung

$(x_{1}-p_{1})\cdot n_{1}+(x_{2}-p_{2})\cdot n_{2}+(x_{3}-p_{3})\cdot n_{3}=0$ .

Ist beispielsweise (siehe Bild) der Stützvektor ${\vec {p}}=(3,2,1)^{T}$ und der Normalenvektor ${\vec {n}}=(2,-1,2)^{T}$ , so erhält man als Ebenengleichung

$(x-3)\cdot 2+(y-2)\cdot (-1)+(z-1)\cdot 2=0\;\;\Rightarrow$

$2x-y+2z=6.$

Jede Wahl von (x,y,z) , die die Ebenengleichung erfüllt, beispielsweise (2,0,1) oder (1,2,3) , entspricht dann einem Ebenenpunkt.

Berechnung

Aus der Parameterform

Aus der Parameterform einer Ebenengleichung mit den beiden Richtungsvektoren ${\vec {u}}$ und ${\vec {v}}$ lässt sich ein Normalenvektor der Ebene durch Berechnung des Kreuzprodukts

${\vec {n}}={\vec {u}}\times {\vec {v}}$

bestimmen. Der Stützvektor ${\vec {p}}$ kann aus der Parameterform übernommen werden.

Aus der Dreipunkteform

Aus der Dreipunkteform einer Ebenengleichung werden zunächst zwei Richtungsvektoren als Differenzvektoren zwischen den Ortsvektoren ${\vec {p}}$ , ${\vec {q}}$ und ${\vec {r}}$ jeweils zweier Punkte ermittelt und dann wie bei der Parameterform das Kreuzprodukt

${\vec {n}}=({\vec {q}}-{\vec {p}})\times ({\vec {r}}-{\vec {p}})$

berechnet. Als Stützvektor ${\vec {p}}$ kann der Ortsvektor einer der Punkte verwendet werden.

Aus der Koordinatenform

Aus der Koordinatenform einer Ebenengleichung mit den Parametern a,b,c und lässt sich ein Normalenvektor der Ebene als

${\vec {n}}={\begin{pmatrix}a\\b\\c\end{pmatrix}}$

ablesen. Einen Stützvektor erhält man, je nachdem welche der Zahlen a,b,c ungleich null ist, durch Wahl von

${\vec {p}}={\begin{pmatrix}d/a\\0\\0\end{pmatrix}},~{\vec {p}}={\begin{pmatrix}0\\d/b\\0\end{pmatrix}}$ oder ${\vec {p}}={\begin{pmatrix}0\\0\\d/c\end{pmatrix}}$ .

Analog lässt sich auf diese Weise auch aus der Achsenabschnittsform einer Ebenengleichung ein Normalenvektor und ein Stützvektor ermitteln.

Herleitung

Zur Herleitung der Normalenform einer Ebenengleichung

Der Ortsvektor ${\vec {x}}$ eines beliebigen Geraden- oder Ebenenpunkts lässt sich als Summe

${\vec {x}}={\vec {x}}_{s}+{\vec {x}}_{p}$

darstellen, wobei ${\vec {x}}_{s}$ senkrecht zur Gerade oder Ebene, also parallel zu ${\vec {n}}$ , und ${\vec {x}}_{p}$ parallel zur Gerade oder Ebene, also senkrecht zu ${\vec {n}}$ , verläuft. Dann ist

${\vec {x}}\cdot {\vec {n}}=({\vec {x}}_{p}+{\vec {x}}_{s})\cdot {\vec {n}}={\vec {x}}_{p}\cdot {\vec {n}}+{\vec {x}}_{s}\cdot {\vec {n}}={\vec {x}}_{s}\cdot {\vec {n}}$ ,

da ${\vec {x}}_{p}\cdot {\vec {n}}$ als Skalarprodukt zueinander senkrechter Vektoren stets null ist. Der Anteil ${\vec {x}}_{s}$ ist aber für jeden auf der Gerade oder Ebene liegenden Punkt der gleiche, also ist für jeden Punkt der Gerade oder Ebene ${\vec {x}}\cdot {\vec {n}}={\vec {x}}_{s}\cdot {\vec {n}}$ konstant. Damit folgt die Normalenform

${\vec {x}}\cdot {\vec {n}}-{\vec {p}}\cdot {\vec {n}}=({\vec {x}}-{\vec {p}})\cdot {\vec {n}}=0$ ,

wobei ${\vec {p}}$ ein beliebig ausgewählter Punkt auf der Gerade oder Ebene ist.

Verallgemeinerung

Allgemein wird durch eine Normalengleichung eine Hyperebene im -dimensionalen euklidischen Raum beschrieben. Im -dimensionalen euklidischen Raum besteht eine Hyperebene entsprechend aus denjenigen Punkten, deren Ortsvektoren ${\vec {x}}$ die Gleichung

$({\vec {x}}-{\vec {p}})\cdot {\vec {n}}=0$

beziehungsweise

${\vec {x}}\cdot {\vec {n}}={\vec {p}}\cdot {\vec {n}}$

erfüllen. Es wird dabei lediglich mit -komponentigen statt mit zwei- oder dreikomponentigen Vektoren gerechnet. Eine Hyperebene teilt den -dimensionalen Raum in zwei Teile, die Halbräume genannt werden. Gilt ${\vec {x}}\cdot {\vec {n}}>{\vec {p}}\cdot {\vec {n}}$ , dann liegt der Punkt in demjenigen Halbraum, in den der Normalenvektor zeigt, ansonsten in dem anderen. Ein Punkt, dessen Ortsvektor die Normalengleichung erfüllt, liegt genau auf der Hyperebene.

Lösbarkeit von linearen Gleichungssystemen

Jede Gleichung eines linearen Gleichungssystems lässt sich als Normalenform einer Hyperebene in einem n-dimensionalen Vektorraum deuten, wobei n die Anzahl der Variablen bzw. Unbekannten ist. Für n=2 sind dies Geraden in der Ebene, für n=3 Ebenen im Raum. Damit lässt sich die Lösbarkeit eines linearen Gleichungssystems zurückführen auf ein Schnittproblem von Hyperebenen: Gesucht ist die Menge der gemeinsamen Punkte aller Hyperebenen. Aus der Lage der Normalenvektoren und damit der Hyperebenen zueinander kann auf die Lösbarkeit des linearen Gleichungssystems und auf die Anzahl der Lösungen geschlossen werden.

Literatur

Lothar Papula: Mathematische Formelsammlung: Für Ingenieure und Naturwissenschaftler. Springer, 2009, ISBN 978-3-8348-9598-1.
Harald Scheid, Wolfgang Schwarz: Elemente Der Linearen Algebra Und Der Analysis. Springer, 2009, ISBN 978-3-8274-2255-2.

Basierend auf einem Artikel in:

Wikipedia.de