Kardioide

Kardioide erzeugt durch einen rollenden Kreis auf einem Kreis mit demselben Radius.

Erzeugung einer Kardioide durch Abrollen eines Kreises auf einem Kreis mit gleichem Radius

Die Kardioide oder Herzkurve (von griechisch καρδία ‚Herz‘; englisch:Cardioid) ist eine ebene Kurve, genauer gesagt eine algebraische Kurve 4. Ordnung, die ihren Namen wegen ihrer Form erhielt.

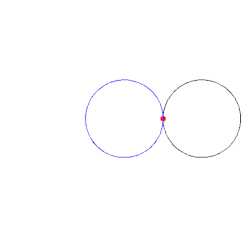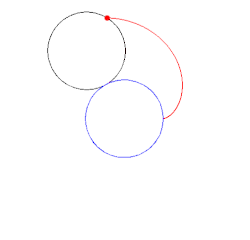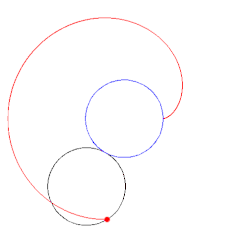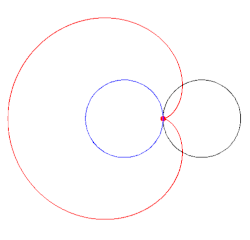
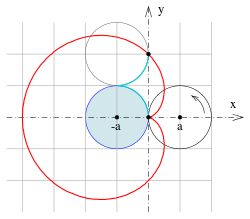
Lässt man auf der Außenseite eines gegebenen festen Kreises mit Mittelpunkt M und Radius einen weiteren Kreis mit dem gleichen Radius abrollen und betrachtet man dabei einen bestimmten Punkt P auf dem abrollenden Kreis, so beschreibt P eine Kardioide. Damit erweist sich die Kardioide als spezielle Epizykloide.

Gleichungen der Kardioide

Ist der gemeinsame Radius der erzeugenden Kreise mit den Mittelpunkten $(-a,0),(a,0)$ , $\varphi$ der Rollwinkel und der Nullpunkt der Startpunkt (s. Bild), so erhält man die

Parameterdarstellung:

$x(\varphi )=2a(1-\cos \varphi )\cdot \cos \varphi \ ,$

$y(\varphi )=2a(1-\cos \varphi )\cdot \sin \varphi \ ,\qquad 0\leq \varphi <2\pi$ .

Hieraus ergibt sich die Darstellung in

Polarkoordinaten:

$r(\varphi )=2a(1-\cos \varphi )$

Mit der Substitution $\cos \varphi =x/r$ und $r={\sqrt {x^{2}+y^{2}}}$ erhält man nach Beseitigung der Wurzel die implizite Darstellung in

Kartesische Koordinaten:

$(x^{2}+y^{2})^{2}+4ax(x^{2}+y^{2})-4a^{2}y^{2}\,=\,0$ .

Beweis der Parameterdarstellung

Der Beweis der Parameterdarstellung lässt sich mit Hilfe komplexer Zahlen und ihrer Darstellung als Gaußsche Zahlenebene leicht führen. Die Rollbewegung des schwarzen Kreises auf dem blauen Kreis kann man in die Hintereinanderausführung zweier Drehungen zerlegen. Die Drehung eines Punktes (komplexe Zahl) um den Nullpunkt $0$ mit dem Winkel $\varphi$ wird durch die Multiplikation mit $e^{i\varphi }$ bewirkt.

Die Drehung $\Phi _{+}$ um den Punkt ist $z\mapsto a+(z-a)e^{i\varphi }$ .

Die Drehung $\Phi _{-}$ um den Punkt

ist $z\mapsto -a+(z+a)e^{i\varphi }$ .

Ein Kardioidenpunkt $p(\varphi )$ entsteht durch Drehung des Nullpunktes um und anschließende Drehung um jeweils um den Winkel $\varphi$ :

$p(\varphi )=\Phi _{-}(\Phi _{+}(0))=\Phi _{-}(a-ae^{i\varphi })=-a+(a-ae^{i\varphi }+a)e^{i\varphi }=a\;(-e^{i2\varphi }+2e^{i\varphi }-1)$ .

hieraus ergibt sich

${\begin{array}{cclcccc}x(\varphi )&=&a\;(-\cos(2\varphi )+2\cos \varphi -1)&=&2a(1-\cos \varphi )\cdot \cos \varphi &&\\y(\varphi )&=&a\;(-\sin(2\varphi )+2\sin \varphi )&=&2a(1-\cos \varphi )\cdot \sin \varphi &.&\end{array}}$

(Es wurden die Formeln $e^{i\varphi }=\cos \varphi +i\sin \varphi ,\ (\cos \varphi )^{2}+(\sin \varphi )^{2}=1,\ \cos 2\varphi =(\cos \varphi )^{2}-(\sin \varphi )^{2},\;\sin 2\varphi =2\sin \varphi \cos \varphi$ benutzt. Siehe Formelsammlung Trigonometrie.)

Flächeninhalt, Kurvenlänge und Krümmungsradius

Für die obige Kardioide ist

der Flächeninhalt $A=6\pi a^{2}$ , und
die Kurvenlänge $L=16a$ .
Krümmungsradius $\rho (\varphi )={\tfrac {8}{3}}a\sin {\tfrac {\varphi }{2}}\ .$

Die Beweise verwenden jeweils die Polardarstellung der obigen Kardioide. Formeln für den Flächeninhalt und die Kurvenlänge findet man z.B. hier.

Beweis für den Flächeninhalt: $A=2\cdot {\tfrac {1}{2}}\int _{0}^{\pi }{(r(\varphi ))^{2}}\;d\varphi =\int _{0}^{\pi }{4a^{2}(1-\cos \varphi )^{2}}\;d\varphi =\cdots =4a^{2}\cdot {\tfrac {3}{2}}\pi =6\pi a^{2}$ .
Beweis für die Kurvenlänge: $L=2\int _{0}^{\pi }{\sqrt {r(\varphi )^{2}+(r'(\varphi ))^{2}}}\;d\varphi =\cdots =8a\int _{0}^{\pi }{\sqrt {{\tfrac {1}{2}}(1-\cos \varphi )}}\;d\varphi =8a\int _{0}^{\pi }\sin({\tfrac {\varphi }{2}})d\varphi =16a$ .
Beweis für den Krümmungsradius

Der Krümmungsradius $\rho$ einer Kurve in Polarkoordinaten $r=r(\varphi )$ ist (s. Krümmung)

$\rho (\varphi )={\frac {\left[r(\varphi )^{2}+{\dot {r}}(\varphi )^{2}\right]^{3/2}}{r(\varphi )^{2}+2{\dot {r}}(\varphi )^{2}-r(\varphi ){\ddot {r}}(\varphi )}}\ .$

Für die Kardioide $r(\varphi )=2a(1-\cos \varphi )=4a\sin ^{2}{\tfrac {\varphi }{2}}$ ergibt sich

$\rho (\varphi )=\cdots ={\frac {[16a^{2}\sin ^{2}{\frac {\varphi }{2}}]^{\frac {3}{2}}}{24a^{2}\sin ^{2}{\frac {\varphi }{2}}}}={\frac {8}{3}}a\sin {\frac {\varphi }{2}}\ .$

Eigenschaften der Kardioide

Sehnen einer Kardioide

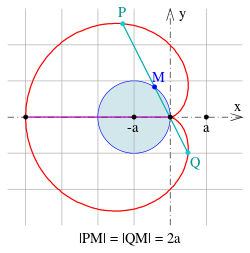
Sehnen durch die Spitze

S1: Die Sehnen durch die Spitze der Kardioide haben alle dieselbe Länge $4a$ .

S2: Die Mittelpunkte der Sehnen durch die Spitze liegen auf dem festen Erzeugerkreis (s. Bild).

Beweis zu S1

Die Punkte $P:p(\varphi ),\;Q:p(\varphi +\pi )$ liegen auf einer Sehne durch die Spitze (=Nullpunkt). Es ist

$|PQ|=r(\varphi )+r(\varphi +\pi )$

$=2a(1-\cos \varphi )+2a(1-\cos(\varphi +\pi ))=\cdots =4a$ .

Beweis zu S2

Für den Beweis wird die Darstellung in der gaußschen Zahlenebene (s. o.) verwendet. Für die Punkte

$P:p(\varphi )=a\;(-e^{i2\varphi }+2e^{i\varphi }-1)$

$Q:p(\varphi +\pi )=a\;(-e^{i2(\varphi +\pi )}+2e^{i(\varphi +\pi )}-1)=a\;(-e^{i2\varphi }-2e^{i\varphi }-1)$ ,

ist

$M:{\tfrac {1}{2}}(p(\varphi )+p(\varphi +\pi ))=\cdots =-a-ae^{i2\varphi }$

der Mittelpunkt der Sehne und liegt auf dem Kreis der Gaußschen Zahlenebene mit Mittelpunkt und Radius (s. Bild).

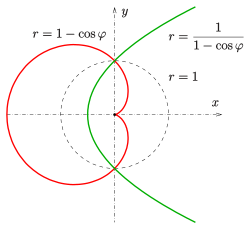
Die Kardioide entsteht durch Spiegelung einer Parabel am Einheitskreis (gestrichelt)

Kardioide als inverse Kurve einer Parabel

→ Hauptartikel: Inversion (Geometrie)

Die Kardioide ist das Bild einer Parabel unter einer Kreisspiegelung (Inversion), bei der das Inversionszentrum im Brennpunkt der Parabel liegt (s. Bild).

Im Beispiel des Bildes haben die Erzeugerkreise den Radius $a={\tfrac {1}{2}}$ . Die gespiegelte Parabel genügt in x-y-Koordinaten der Gleichung $x={\tfrac {1}{2}}(y^{2}-1)$ .

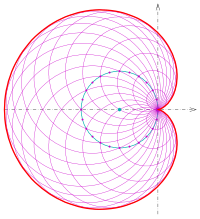
Kardioide als Einhüllende einer Kreisschar

Bildet man bei der Inversion der Parabel im vorigen Abschnitt die Tangenten mit ab, so gehen sie als Geraden in eine Schar von Kreisen durch das Inversionszentrum (Nullpunkt) über. Eine genauere Untersuchung (Nachrechnen) zeigt: Die Mittelpunkte der Kreise liegen alle auf dem festen Erzeugerkreis (cyan) der Kardioide. Der Erzeugerkreis ist das Bild der Leitlinie der Parabel. Da sich auf der Leitlinie einer Parabel die Tangenten senkrecht schneiden und die Kreisspiegelung winkeltreu ist, schneiden sich Kreise der Kreisschar auf dem Erzeugerkreis auch senkrecht.

Die hier beschriebene Eigenschaft der Kreisschar erlaubt eine einfache Methode um eine Kardioide zu zeichnen:

1) Wähle einen Kreis k und einen Punkt O darauf,

2) zeichne Kreise durch O mit Mittelpunkte auf k,

3) zeichne die Einhüllende dieser Kreise.

Beweis mit Einhüllenden-Bedingung

Es sei durch

$F(x,y,t)=0$

eine Schar von impliziten Kurven mit dem Scharparameter gegeben. Die Einhüllende (oder Hüllkurve) besteht aus Punkten (x,y) , die für festes Lösungen des i.a. nicht linearen Gleichungssystems

$F(x,y,t)=0,\quad F_{t}(x,y,t)=0\;.$ (Einhüllenden-Bedingungen)

sind. ( $F_{t}$ bedeutet die partielle Ableitung nach , siehe Einhüllende)

Es sei k der Kreis mit Mittelpunkt (-1,0) und Radius . k hat die Parameterdarstellung $(-1+\cos t,\sin t)$ . Die Kreisschar, deren Mittelpunkte auf k liegen und die durch den Punkt $O=(0,0)$ gehen, lassen sich implizit durch

$F(x,y,t)=(x+1-\cos t)^{2}+(y-\sin t)^{2}-(2-2\cos t)=0$

beschreiben. Multipliziert man die Klammern aus, ergibt sich

$F(x,y,t)=x^{2}+y^{2}+2x\;(1-\cos t)-2y\;\sin t=0\;.$ Die 2. Scharbedingung ist

$F_{t}(x,y,t)=2x\;\sin t-2y\;\cos t=0$

Man prüft leicht nach, dass die Punkte der Kardioide mit der Parameterdarstellung

$x(t)=2(1-\cos t)\cos t,\quad y(t)=2(1-\cos t)\sin t$

das nicht lineare Gleichungssystem erfüllt. Der Scharparameter ist hier identisch mit dem Winkel-Parameter der Kardioide.

Kardioide als Einhüllende einer Geradenschar

Kardioide als Einhüllende einer Geradenschar

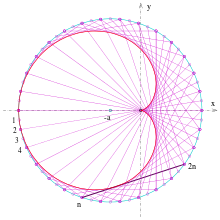
Eine ähnlich einfache Methode, eine Kardioide als Einhüllende einer Geradenschar zu konstruieren, geht auf L. Cremona zurück:

Zeichne einen Kreis, unterteile ihn gleichmäßig mit Punkten (s. Bild) und nummeriere diese fortlaufend.
Zeichne die Sehnen: $(1,2),(2,4),....,(n,2n),....,(N,2N),(N+1,2),(N+2,4),....,$ . (Man kann es so ausdrücken: Der zweite Punkt der Sehne bewegt sich mit doppelter Geschwindigkeit.)
Die Einhüllende dieser Strecken ist eine Kardioide.

Kardioide: Erzeugung nach Cremona, zum Beweis

Beweis

Im Folgenden werden die trigonometrischen Formeln für $\cos \alpha +\cos \beta ,\ \sin \alpha +\sin \beta ,\ 1+\cos 2\alpha ,\ \cos 2\alpha ,\sin 2\alpha$ verwendet. Um die Rechnungen einfach zu halten, wird der Beweis für die Kardioide mit der Polardarstellung $r=2(1{\color {red}+}\cos \varphi )$ geführt (s. Abschnitt anders orientierte Kardioiden).

Gleichung der Tangente: an die Kardioide mit der Polardarstellung $r=2(1+\cos \varphi )$ :; Aus der Parameterdarstellung; $x(\varphi )=2(1+\cos \varphi )\cos \varphi ,$; $y(\varphi )=2(1+\cos \varphi )\sin \varphi$

berechnet man zunächst den Normalenvektoren ${\vec {n}}=({\dot {y}},-{\dot {x}})^{T}$ . Die Gleichung der Tangente ${\dot {y}}(\varphi )\cdot (x-x(\varphi ))-{\dot {x}}(\varphi )\cdot (y-y(\varphi ))=0$ ist dann:

$(\cos 2\varphi +\cos \varphi )\cdot x\ +\ (\sin 2\varphi +\sin \varphi )\cdot y=2(1+\cos \varphi )^{2}\ .$

Mit Hilfe der trigonometrischen Formeln und der anschließenden Division durch $\cos {\tfrac {1}{2}}\varphi$ lässt sich die Gleichung der Tangente so schreiben:

$\cos({\tfrac {3}{2}}\varphi )\cdot x+\sin({\tfrac {3}{2}}\varphi )\cdot y=4(\cos {\tfrac {1}{2}}\varphi )^{3}\quad 0<\varphi <2\pi ,\ \varphi \neq \pi .$

Gleichung der Sekante: an den Kreis mit Mittelpunkt und Radius : Für die Gleichung der Sekante durch die beiden Punkte $(1+3\cos \theta ,3\sin \theta ),\ (1+3\cos {\color {red}2}\theta ,3\sin {\color {red}2}\theta ))$ ergibt sich:; $(\sin \theta -\sin 2\theta )\cdot x\ +\ (\cos 2\theta -\sin \theta )\cdot y=-2\cos \theta -\sin 2\theta \ .$

Mit Hilfe der trigonometrischen Formeln und der anschließenden Division durch $\sin {\tfrac {1}{2}}\theta$ lässt sich die Gleichung der Sekante so schreiben:

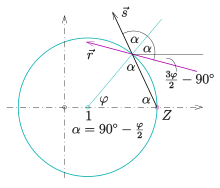
$\cos({\tfrac {3}{2}}\theta )\cdot x+\sin({\tfrac {3}{2}}\theta )\cdot y=4(\cos {\tfrac {1}{2}}\theta )^{3}\quad 0<\theta <2\pi .$

Die beiden Winkel $\varphi ,\theta$ haben zwar verschiedene Bedeutungen (s. Bild), für $\varphi =\theta$ ergibt sich aber dieselbe Gerade. Also ist auch jede obige Sekante an den Kreis eine Tangente der Kardioide und

die Kardioide ist die Einhüllende der Kreissehnen.

Bemerkung:
Der Beweis lässt sich auch mit den Einhüllen-Bedingungen einer impliziten Kurvenschar (s. vorigen Abschnitt) führen. Dabei beschreibt

$F(x,y,t)=\cos {\tfrac {3}{2}}t\cdot x\ +\ \sin {\tfrac {3}{2}}t\cdot y-4(\cos {\tfrac {1}{2}}t)^{3}=0\ ,$ die Schar der Sekanten an den Kreis (s.o.)

$F_{t}(x,y,t)=-{\tfrac {3}{2}}\sin {\tfrac {3}{2}}t\cdot x\ +\ {\tfrac {3}{2}}\cos {\tfrac {3}{2}}t\cdot y+3\cos {\tfrac {1}{2}}t\sin t=0\ .$

Beide Gleichungen sind für festen Parameter t Geradengleichungen. Der Schnittpunkt

$x(t)=2(1+\cos t)\cos t,\quad y(t)=2(1+\cos t)\sin t$

der Geraden ist ein Punkt der Kardioide mit der Polardarstellung $r=2(1+\cos t)$ . (Bei Umformungen müssen immer wieder trigonometrische Formeln (s.o.) benutzt werden.)

Zu Kardioide als Kaustik:
Lichtquelle , Lichtstrahl ${\vec {s}}$ , reflektierter Strahl ${\vec {r}}$

Kardioide als Kaustik eines Kreises mit Lichtquelle (rechts) auf dem Kreis

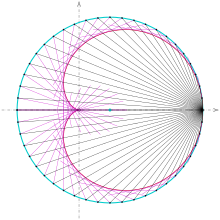
Kardioide als Kaustik eines Kreises

Die vorigen Überlegungen liefern auch einen Beweis dafür, dass als Kaustik eines Kreises mit der Lichtquelle auf dem Kreis eine Kardioide auftritt.

Gehen in der Ebene von einem Punkt eines spiegelnden Kreises Lichtstrahlen gemäß der Abbildung aus, so sind die im Innern des Kreises reflektierten Lichtstrahlen die Tangenten einer Kardioide. (s. Abschnitt Kardioide in Optik und Akustik)

Beweis

Der Kreis habe (wie im vorigen Abschnitt) den Mittelpunkt $(1,0)$ und den Radius . Der Kreis hat dann die Parameterdarstellung

$k(\varphi )=(1+3\cos \varphi ,3\sin \varphi )\ .$

Die Tangente im Kreispunkt $K=k(\varphi )$ hat den Normalenvektor ${\vec {n}}_{t}=(\cos \varphi ,\sin \varphi )^{T}$ . Der reflektierte Strahl muss dann (laut Abbildung) den Normalenvektor ${\vec {n}}_{r}=(\cos {\color {red}{\tfrac {3}{2}}}\varphi ,\sin {\color {red}{\tfrac {3}{2}}}\varphi )^{T}$ haben und durch den Kreispunkt $K:(1+3\cos \varphi ,3\sin \varphi )$ gehen. Der reflektierte Strahl liegt also (s. vorigen Abschnitt) auf der Gerade mit der Gleichung

$\cos {\tfrac {3}{2}}\varphi \cdot x\ +\ \sin {\tfrac {3}{2}}\varphi \cdot y=4(\cos {\tfrac {1}{2}}\varphi )^{3}\ ,$

die wiederum Tangente an die Kardioide mit der Polardarstellung

$r=2(1+\cos \varphi )$

des vorigen Abschnitts ist.

Bemerkung: Mehrfachreflexionen am Kreis werden bei diesen Überlegungen üblicherweise nicht berücksichtigt.

Kardioide als Fußpunktkurve eines Kreises

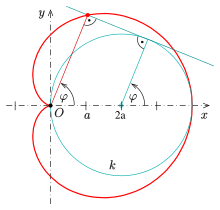
Kardioide: Lotfußpunkte auf Kreistangenten

Die Cremona-Erzeugung einer Kardioide sollte nicht verwechselt werden mit der folgenden Erzeugung:

Es sei ein Kreis und ein fester Punkt auf diesem Kreis gegeben. Es gilt:

Die Lotfußpunkte vom Punkt auf die Tangenten des Kreises bilden eine Kardioide.

Eine Kardioide ist somit eine spezielle Fußpunktkurve (engl.: pedal curve) eines Kreises.

Beweis

In der x-y-Ebene habe der Kreis den Mittelpunkt $(2a,0)$ und den Radius . Die Tangente im Kreispunkt $(2a+2a\cos \varphi ,2a\sin \varphi )$ hat die Gleichung

$(x-2a)\cdot \cos \varphi +y\cdot \sin \varphi =2a\ .$

Der Lotfußpunkt von auf die Tangente ist der Punkt $(r\cos \varphi ,r\sin \varphi )$ mit dem noch unbekannten Abstand zum Nullpunkt . Einsetzen in die Tangentengleichung ergibt

$(r\cos \varphi -2a)\cos \varphi +r\sin ^{2}\varphi =2a\quad \rightarrow \quad r=2a(1+\cos \varphi )$

die Polardarstellung einer Kardioide.

Bemerkung: Liegt der Punkt nicht auf dem Kreis , so entsteht eine pascalsche Schnecke (s. nächsten Abschnitt).

Kardioide als pascalsche Schnecke

Eine pascalsche Schnecke ist eine ebene Kurve mit einer Polardarstellung $r=b+a\cos t$ . Im Fall $b=a$ ergibt sich eine Kardioide. Also gilt:

Die Kardioide ist ein Spezialfall der pascalschen Schnecke, diese ist wiederum ein Spezialfall der Konchoide.

Kardioide auf der Glasur eines Schmortopfes

Kardioide in Optik und Akustik

Die Lichterscheinung (Kaustik) in einer Kaffeetasse, die von Licht aus einer am Tassenrand platzierten Lichtquelle getroffen wird, ist eine Kardioide. Die Kaustik, die von parallel eintreffendem Licht erzeugt wird, wird allerdings durch eine andere Kurve (Nephroide) beschrieben; in anderen Fällen entsteht eine Mischform.

In der Tontechnik wird das Polardiagramm der Richtcharakteristik einer Kardioide mit Niere bezeichnet, auch wenn es eine Herzkurve darstellt.

Evolute einer Kardioide

Evolute (grün) einer Kardioide (rot)
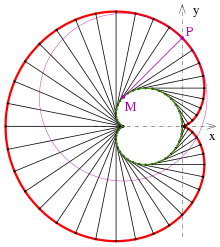
magenta: ein Punkt P, sein Krümmungsmittelpunkt M und der zugehörige Krümmungskreis

Die Evolute einer ebenen Kurve ist der geometrische Ort aller Krümmungsmittelpunkte dieser Kurve. Für eine parametrisierte Kurve ${\vec {x}}(s)={\vec {c}}(s)$ mit Krümmungsradius $\rho (s)$ hat die Evolute die Parameterdarstellung

${\vec {X}}(s)={\vec {c}}(s)+\rho (s){\vec {n}}(s).$

wobei ${\vec n}(s)$ die geeignet orientierte Einheitsnormale ist. ( ${\vec n}(s)$ zeigt zu dem Krümmungsmittelpunkt hin.)

Für eine Kardioide gilt:

Die Evolute einer Kardioide ist wieder eine Kardioide ein Drittel so groß (siehe Bild).

Beweis

Für die Kardioide mit der Parameterdarstellung

$x(\varphi )=2a(1-\cos \varphi )\cos \varphi =4a\sin ^{2}{\tfrac {\varphi }{2}}\cos \varphi \ ,$

$y(\varphi )=2a(1-\cos \varphi )\sin \varphi =4a\sin ^{2}{\tfrac {\varphi }{2}}\sin \varphi$

ist die Einheitsnormale

${\vec {n}}(\varphi )=(-\sin {\tfrac {3}{2}}\varphi ,\cos {\tfrac {3}{2}}\varphi )$

und der Krümmungskreisradius (s. oben)

$\rho (\varphi )={\tfrac {8}{3}}a\sin {\tfrac {\varphi }{2}}\ .$

Also hat die Evolute die Parameterdarstellung

$X(\varphi )=4a\sin ^{2}{\tfrac {\varphi }{2}}\cos \varphi -{\tfrac {8}{3}}a\sin {\tfrac {\varphi }{2}}\cdot \sin {\tfrac {3}{2}}\varphi =\cdots ={\tfrac {4}{3}}a\cos ^{2}{\tfrac {\varphi }{2}}\cos \varphi -{\tfrac {4}{3}}a\ ,$

$Y(\varphi )=4a\sin ^{2}{\tfrac {\varphi }{2}}\sin \varphi +{\tfrac {8}{3}}a\sin {\tfrac {\varphi }{2}}\cdot \cos {\tfrac {3}{2}}\varphi \ =\cdots ={\tfrac {4}{3}}a\cos ^{2}{\tfrac {\varphi }{2}}\sin \varphi \ .$

Diese Gleichungen beschreiben eine Kardioide, die ein Drittel so groß wie die gegebene Kardioide, um 180 Grad gedreht und um $-{\tfrac {4}{3}}a$ entlang der x-Achse verschoben ist.

(Es wurden trigonometrische Formeln benutzt: $\sin {\tfrac {3}{2}}\varphi =\sin {\tfrac {\varphi }{2}}\cos \varphi +\cos {\tfrac {\varphi }{2}}\sin \varphi \ ,\ \cos {\tfrac {3}{2}}\varphi =\cdots ,\ \sin \varphi =2\sin {\tfrac {\varphi }{2}}\cos {\tfrac {\varphi }{2}}\ ,\ \cos \varphi =\cdots$ .)

Orthogonaltrajektorien

orthogonale Kardioiden

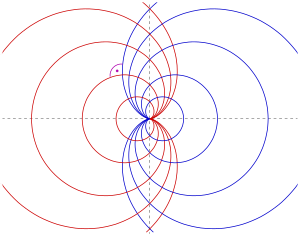
Eine Orthogonaltrajektorie einer Kurvenschar ist eine Kurve, die jede Kurve der Schar senkrecht schneidet. Für Kardioiden gilt:

Die Orthogonaltrajektorien der Kardioidenschar mit den Gleichungen

$r=2a(1-\cos \varphi )\ ,\;a>0\ ,\$

sind die Kardioiden mit den Gleichungen

$r=2b(1+\cos \varphi )\ ,\;b>0\ .$

(Die zweite Schar entsteht durch Spiegelung der ersten an der y-Achse. Siehe Bild.)

Beweis:
Ist eine Kurve in Polarkoordinaten durch eine Funktion $r(\varphi )$ gegeben, so besteht zwischen den kartesischen Koordinaten und den Polarkoordinaten eines Punktes die folgende Beziehung:

$x(\varphi )=r(\varphi )\cos \varphi \ ,\qquad$ $y(\varphi )=r(\varphi )\sin \varphi \qquad$

und damit

${\frac {dx}{d\varphi }}=r'(\varphi )\cos \varphi -r(\varphi )\sin \varphi \ ,\qquad$ ${\frac {dy}{d\varphi }}=r'(\varphi )\sin \varphi +r(\varphi )\cos \varphi \ .$

Dividiert man die letzten beiden Gleichungen erhält man die Steigung in kartesischen Koordinaten:

${\frac {dy}{dx}}={\frac {r'(\varphi )\sin \varphi +r(\varphi )\cos \varphi }{r'(\varphi )\cos \varphi -r(\varphi )\sin \varphi }}.$

Für die Kardioiden mit den Gleichungen $r=2a(1-\cos \varphi )\;$ bzw. $r=2b(1+\cos \varphi )\$ ergibt sich

${\frac {dy_{a}}{dx}}={\frac {\cos \varphi -\cos 2\varphi }{\sin 2\varphi -\sin \varphi }}\quad$ bzw. $\quad {\frac {dy_{b}}{dx}}=-{\frac {\cos \varphi +\cos 2\varphi }{\sin 2\varphi +\sin \varphi }}\ .$

(Die Steigungen hängen jeweils nur von $\varphi$ ab, und nicht mehr von den Parametern a,b !)
Hieraus ergibt sich

${\frac {dy_{a}}{dx}}\cdot {\frac {dy_{b}}{dx}}=\cdots =-{\frac {\cos ^{2}\varphi -\cos ^{2}2\varphi }{\sin ^{2}2\varphi -\sin ^{2}\varphi }}=-{\frac {-1+\cos ^{2}\varphi +1-\cos ^{2}2\varphi }{\sin ^{2}2\varphi -\sin ^{2}\varphi }}=-1\ .$

D.h. jede Kurve der einen Schar schneidet jede Kurve der anderen Schar senkrecht.

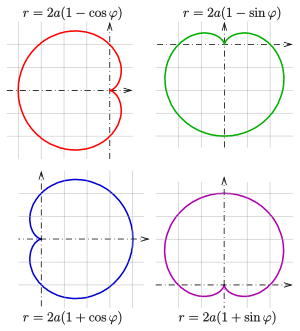
4 Kardioiden mit Polardarstellung und Lage im Koordinatensystem

Anders orientierte Kardioiden

Wählt man andere Lagen der Kardioide im Koordinatensystem so ändern sich die Gleichungen, die sie beschreiben. Im Bild sind die 4 üblichen Orientierungen und ihre zugehörigen Polardarstellungen zu sehen.

Zur Geschichte der Kardioide

Bei der Suche nach einer optimalen Form von Zahnrädern untersuchte Ole Roemer 1674 Epizykloiden und damit auch Kardioiden. Der Name Kardioide wurde zuerst von Johann Francesco Melchiore Salvemini Castillon verwendet. Die Länge einer Kardioide wurde 1708 von Philippe de la Hire berechnet. Eine Kardioide ist eine spezielle Pascalsche Schnecke, benannt nach Étienne Pascal, dem Vater von Blaise Pascal.

Literatur

Kleine Enzyklopädie Mathematik. Harri Deutsch-Verlag, 1977, ISBN 3-87144-323-9.

Basierend auf einem Artikel in:

Wikipedia.de