Partielle Ableitung

In der Differentialrechnung ist eine partielle Ableitung die Ableitung einer Funktion mit mehreren Argumenten nach einem dieser Argumente (in Richtung dieser Koordinatenachse). Die Werte der übrigen Argumente werden also konstant gehalten.

Definition

Erster Ordnung

Sei eine offene Teilmenge des euklidischen Raums $\mathbb {R} ^{n}$ und $f\colon U\rightarrow \mathbb {R}$ eine Funktion. Sei weiterhin ein Element $a=(a_{1},\dotsc ,a_{n})$ in gegeben. Falls für die natürliche Zahl mit $1 \leq i \leq n$ der Grenzwert

${\frac {\partial f}{\partial x_{i}}}(a):=\lim _{h\to 0}{\frac {f(a_{1},\dotsc ,a_{i}+h,\dotsc ,a_{n})-f(a_{1},\dotsc ,a_{i},\dotsc ,a_{n})}{h}}$

existiert, dann nennt man ihn die partielle Ableitung von nach der -ten Variablen $x_{i}$ im Punkt . Die Funktion heißt dann im Punkt partiell differenzierbar. Das Symbol ∂ (es ähnelt dem kursiven Schnitt der kyrillischen Minuskel д) wird als oder zur Unterscheidung auch del ausgesprochen. Die Schreibweise ${\tfrac {\partial f}{\partial x_{i}}}$ wurde durch Verwendung von C. G. J. Jacobi bekannt.

Dem gegenüber existiert in der Technischen Mechanik eine andere Schreibweise, bei der die Richtung der Funktion mit einem Komma im Index angezeigt wird um von der Richtung des Arguments der Funktion zu unterscheiden: So ist die Ableitung der Verschiebung $u_{{1}}$ (also die Verschiebung in $x_{1}$ -Richtung) folgendermaßen äquivalent ${\frac {\partial u_{1}}{\partial x_{1}}}=u_{1,1}$ . Analog dazu wäre ${\frac {\partial u_{2}}{\partial x_{3}}}=u_{2,3}$ die Ableitung in $x_{3}$ -Richtung einer Verschiebung in $x_{2}$ -Richtung.

Höhere Ordnung

Die partielle Ableitung nach $x_{i}$ ist selbst wieder eine Funktion von nach $\mathbb {R}$ , falls in ganz nach $x_{i}$ partiell differenzierbar ist. Als abkürzende Schreibweise für die partiellen Ableitungen ${\tfrac {\partial f}{\partial x_{i}}}$ ist auch oft $\textstyle\partial_{x_i} f$ , $\textstyle f_{x_i}$ oder D_i f zu finden.

Ist die Funktion $f\colon U\to \mathbb {R}$ in jedem Punkt ihres Definitionsbereichs partiell differenzierbar, so sind die partiellen Ableitungen

$\frac{\partial f}{\partial x_i} \colon a \mapsto \frac{\partial f}{\partial x_i}(a)$

wieder Funktionen von nach $\mathbb {R}$ , die wiederum auf Differenzierbarkeit untersucht werden können. Man erhält so höhere partielle Ableitungen

$\frac{\partial^2 f}{\partial x_j \partial x_i} = \frac{\partial }{\partial x_j}\left(\frac{\partial f}{\partial x_i}\right)$ und $\displaystyle \frac{\partial^2 f}{\partial x_i^2 } = \frac{\partial }{\partial x_i}\left(\frac{\partial f}{\partial x_i}\right)$

Geometrische Deutung

In einem dreidimensionalen Koordinatensystem wird der Funktionsgraph einer Funktion $f\colon U\rightarrow \mathbb {R} ^{+}$ betrachtet. Der Definitionsbereich sei eine offene Teilmenge der xy-Ebene. Ist differenzierbar, dann ist der Graph der Funktion eine Fläche über dem Definitionsbereich .

Für einen festen Wert von ist dann eine Funktion in . Bei festem ergeben die Punkte $\{(x,y): y\in \R \text{ mit } (x,y)\in U\}$ eine Strecke parallel zur -Achse. Diese Strecke wird von auf eine gekrümmte Linie auf dem Graph von projiziert. Die partielle Ableitung von nach entspricht unter diesen Voraussetzungen der Steigung der Tangente an diese Kurve im Punkt f(x,y) .

Sätze und Eigenschaften

Zusammenhang Ableitung, partielle Ableitung, Stetigkeit

Total differenzierbare Funktionen sind stetig.
Total differenzierbare Funktionen sind partiell differenzierbar.
Partiell differenzierbare Funktionen sind nicht notwendigerweise stetig und damit auch nicht notwendigerweise total differenzierbar.
Stetig partiell differenzierbare Funktionen, also Funktionen, deren partielle Ableitungen stetig sind, sind dagegen stetig total differenzierbar.

Satz von Schwarz

Es gilt der Satz von Schwarz: Wenn die zweiten partiellen Ableitungen stetig sind, so kann man die Reihenfolge der Ableitung vertauschen:

$\frac{\partial^2 f}{\partial x_j \partial x_i} =\frac{\partial^2 f}{\partial x_i \partial x_j}\,.$

Verwendung

Die ersten partiellen Ableitungen lassen sich in einem Vektor anordnen, dem Gradienten von :

$\text{grad}\, f = \nabla f:= \left(\frac{\partial f}{\partial x_1}, \ldots, \frac{\partial f}{\partial x_n} \right)^T$

Hierbei ist $\nabla$ der Nabla-Operator.

Die zweiten partiellen Ableitungen lassen sich in einer Matrix anordnen, der Hesse-Matrix

$\operatorname{H}_f= \left(\frac{\partial^2f}{\partial x_i\partial x_j}\right)= \begin{pmatrix} \frac{\partial^2 f}{\partial x_1\partial x_1}&\dots&\frac{\partial^2 f}{\partial x_1\partial x_n}\\ \vdots&\ddots&\vdots\\ \frac{\partial^2 f}{\partial x_n\partial x_1}&\dots&\frac{\partial^2 f}{\partial x_n\partial x_n} \end{pmatrix}$
Es gilt die Taylorformel: Wenn die Funktion $f\colon U \to \R$ -mal stetig partiell differenzierbar ist, so lässt sie sich in der Nähe jedes Punktes $a=(a_{1},\dots ,a_{n})\in U$ durch ihre Taylor-Polynome approximieren:

$f(a + h) = \sum_{s =0}^k\,\sum_{j_1 + \dots + j_n =s} \frac{1}{j_1! \cdots j_n!}\,\frac{\partial^{s}f}{\partial x_1^{j_1} \cdots \partial x_n^{j_n}}(a) \, h_1^{j_1} \cdots h_n^{j_n} + r(a,h)$

mit $h = (h_1, \dots, h_n)$ , wobei das Restglied r(a,h)

für $|h| \to 0$ von höherer als -ter Ordnung verschwindet, das heißt:

$\lim_{|h| \to 0} \frac{|r(a,h)|}{|h|^k} = 0.$

Die Terme zu gegebenem ν ergeben die „Taylorapproximation -ter Ordnung“.

Einfache Extremwertprobleme findet man in der Analysis bei der Berechnung von Maxima und Minima einer Funktion einer reellen Variablen (vgl. hierzu den Artikel über Differentialrechnung). Die Verallgemeinerung des Differentialquotienten auf Funktionen mehrerer Variablen (Veränderlichen, Parameter) ermöglicht die Bestimmung ihrer Extremwerte, und für die Berechnung werden partielle Ableitungen benötigt.

In der Differentialgeometrie benötigt man partielle Ableitungen zur Bestimmung eines totalen Differentials. Anwendungen für totale Differentiale findet man in großem Maße in der Thermodynamik.

Partielle Ableitungen sind darüber hinaus ein wesentlicher Bestandteil der Vektoranalysis. Sie bilden die Komponenten des Gradienten, des Laplace-Operators, der Divergenz und der Rotation in Skalar- und Vektorfeldern. Sie treten auch in der Jacobi-Matrix auf.

Beispiele

Beispiel 1

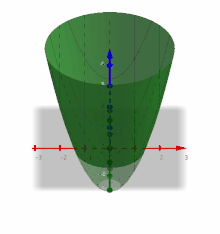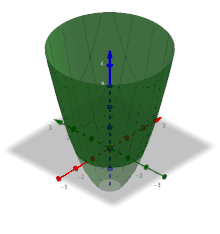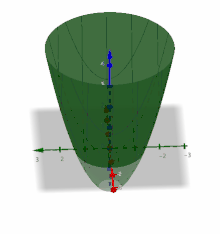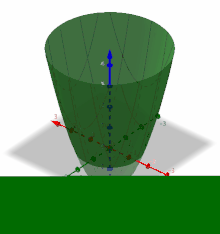
Der Graph von $f(x,y):=x^{2}+y^{2}-2$ ist ein Paraboloid (Animation: GIF-Export Geogebra)

Als Beispiel wird die Funktion $f\colon\R^2\rightarrow\R$ mit $f(x,y):=x^{2}+y^{2}-2$ betrachtet, die von den beiden Variablen und abhängt.

Betrachtet man als eine Konstante, z.B. y = 3 , so hängt die Funktion $g\colon\R\rightarrow\R$ mit g(x)=f(x,3) nur noch von der Variablen ab:

$f(x,3)=x^{2}+7$

Für die neue Funktion gilt folglich $g(x)=x^{2}+7$ und man kann den Differenzialquotienten bilden

$\frac{\mathrm{d}g(x)}{\mathrm{d}x} = \lim_{h \to 0}\frac{g(x+h) - g(x)}{h} = g'(x) = 2 x$

Das gleiche Ergebnis erhält man, wenn man die partielle Ableitung der Funktion nach bildet:

${\frac {\partial f(x,y)}{\partial x}}=\lim _{h\to 0}{\frac {f(x+h,y)-f(x,y)}{h}}=\lim _{h\to 0}{\frac {(x+h)^{2}+y^{2}-2-x^{2}-y^{2}+2}{h}}=2x$

Die partielle Ableitung von nach lautet entsprechend:

${\frac {\partial f(x,y)}{\partial y}}=\lim _{h\to 0}{\frac {f(x,y+h)-f(x,y)}{h}}=\lim _{h\to 0}{\frac {x^{2}+(y+h)^{2}-2-x^{2}-y^{2}+2}{h}}=2y$

Dieses Beispiel demonstriert, wie die partielle Ableitung einer Funktion bestimmt wird, die von mehreren Variablen abhängt:

Bis auf eine Variable werden alle anderen Variablen als konstant angenommen, bezüglich dieser einen Variablen wird der Differenzialquotient bestimmt. Als Ergebnis erhält man die partielle Ableitung der Funktion nach dieser einen Variablen.

Beispiel 2

Da die partielle Ableitung nach einer Variablen der gewöhnlichen Ableitung bei festgehaltenen Werten aller anderen Variablen entspricht, können für die Berechnung alle Ableitungsregeln wie bei Funktionen einer Variablen verwendet werden. Ist beispielsweise

$f(x,y) = x^2 \sin(xy)$ ,

so folgt mit Produkt- und Kettenregel:

$\frac{\partial f(x,y)}{\partial x} = 2x \sin(xy) + x^2 y \cos(xy)$ und

$\frac{\partial f(x,y)}{\partial y} = x^3 \cos(xy)$ .

Beispiel 3

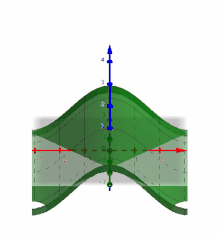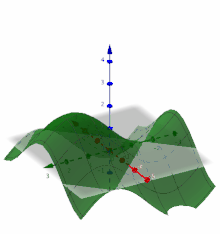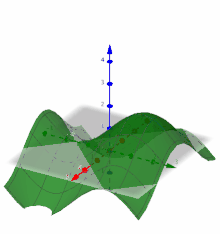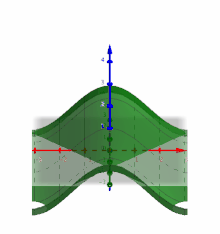
Funktionsplot mit Geogebra $f(x,y):=\cos(x)+\sin(y)$

In der obigen Animation sieht man den Graphen der Funktion $f(x,y)=\cos(x)+\sin(y)$ . Legt man einen Punkt $(x_{o},y_{o})\in \mathbb {R} ^{2}$ aus dem Definitionsbereich fest, so kann man den Graphen der Funktion mit einer senkrechten Ebene in x-Richtung schneiden. Der Schnitt des Graphen mit der Ebene erzeugt einen klassischen Graphen aus der eindimensionalen Analysis. Partielle Ableitungen können so auch anschaulich auf die klassische eindimensionale Analysis zurückgeführt werden.

$f(x,y)=\cos(x)+\sin(y)$ ,

${\frac {\partial f(x,y)}{\partial x}}=-\sin(x)$ und

${\frac {\partial f(x,y)}{\partial y}}=\cos(y)$ .

Partielle und totale Ableitung nach der Zeit

In der Physik (vor allem in der theoretischen Mechanik) tritt häufig die folgende Situation auf: Eine Größe hängt durch eine total differenzierbare Funktion von den Ortskoordinaten , , und von der Zeit ab. Man kann also die partiellen Ableitungen $\tfrac{\partial f}{\partial x}$ , $\tfrac{\partial f}{\partial y}$ , $\tfrac{\partial f}{\partial z}$ und $\tfrac{\partial f}{\partial t}$ bilden. Die Koordinaten eines sich bewegenden Punktes sind durch die Funktionen x(t) , y(t) und z(t) gegeben. Die zeitliche Entwicklung des Werts der Größe am jeweiligen Bahnpunkt wird dann durch die verkettete Funktion

$t \mapsto f(x(t),y(t),z(t),t)$

beschrieben. Diese Funktion hängt nur von einer Variablen, der Zeit , ab. Man kann also die gewöhnliche Ableitung bilden. Diese nennt man die totale oder vollständige Ableitung von nach der Zeit und schreibt dafür auch kurz $\tfrac{\mathrm d f}{\mathrm d t}$ . Sie berechnet sich nach der mehrdimensionalen Kettenregel wie folgt:

$\frac{\mathrm df}{\mathrm dt} = \frac{\mathrm d}{\mathrm dt} f(x(t),y(t),z(t),t) = \frac{\partial f}{\partial x} \frac{\mathrm dx}{\mathrm dt} + \frac{\partial f}{\partial y} \frac{\mathrm dy}{\mathrm dt} + \frac{\partial f}{\partial z} \frac{\mathrm dz}{\mathrm dt} + \frac{\partial f}{\partial t}$

Während bei der partiellen Ableitung $\tfrac{\partial f}{\partial t}$ nach der Zeit nur die explizite Abhängigkeit der Funktion von berücksichtigt wird und alle anderen Variablen konstant gehalten werden, berücksichtigt die totale Ableitung $\tfrac{\mathrm d f}{\mathrm d t}$ auch die indirekte (oder implizite) Abhängigkeit von , die dadurch zustande kommt, dass längs der Bahnbewegung die Ortskoordinaten von der Zeit abhängen.

(Indem man also die implizite Zeitabhängigkeit mitberücksichtigt, redet man im Jargon der Physik auch von „substantieller“ Zeitableitung, bzw. im Jargon der Strömungsmechanik von der Euler-Ableitung im Gegensatz zur Lagrange-Ableitung.)

→ Für eine ausführlichere Darstellung siehe totales Differential

Verallgemeinerung: Richtungsableitung

Eine Verallgemeinerung der partiellen Ableitung stellt die Richtungsableitung dar. Dabei wird die Ableitung in Richtung eines beliebigen Vektors betrachtet und nicht nur in Richtung der Koordinatenachsen.

Literatur

Kurt Endl; Wolfgang Luh: Analysis II, Akademische Verlagsgesellschaft Frankfurt am Main, 1974
Hans Grauert; Wolfgang Fischer: Differential- und Integralrechnung II, 2., verbesserte Auflage, Springer Verlag Berlin, 1978

Basierend auf einem Artikel in:

Wikipedia.de