arctan2

Die mathematische Funktion arctan2, auch atan2, ist eine Erweiterung der inversen Winkelfunktion Arkustangens und wie diese eine Umkehrfunktion der Winkelfunktion Tangens.

Sie nimmt zwei reelle Zahlen als Argumente, im Gegensatz zum normalen Arkustangens, welcher nur eine reelle Zahl zum Argument hat. Damit hat sie genügend Information, um den Funktionswert in einem Wertebereich von $360^{\circ }$ (also allen vier Quadranten) ausgeben zu können, und muss sich nicht (wie der normale Arkustangens) auf zwei Quadranten beschränken. Der volle Wertebereich wird häufig benötigt, beispielsweise bei der Umrechnung ebener kartesischer Koordinaten in Polarkoordinaten: wenn der Funktion $\operatorname {arctan2} (x,y)=:\varphi$ die beiden kartesischen Koordinaten (x,y) als Argumente gegeben werden, erhält man den Polarwinkel $\varphi$ , der sich im richtigen Quadranten befindet, d.h. der die Beziehungen

$x=r\cos \varphi$ und

$y=r\sin \varphi$ mit

$r:=\textstyle {\sqrt {x^{2}+y^{2}}}$

erfüllt. Ein mathematisch nützlicher Zusatzeffekt ist, dass Winkel, bei denen der Tangens eine Polstelle hat, nämlich die Winkel $\pm 90^{\circ }=\pm \pi /2\,,$ durch ganz normale reelle Koordinaten spezifiziert werden können, nämlich durch $\pm \pi /2=\operatorname {arctan2} (0,\pm 1)$ anstatt $\operatorname {arctan} (\pm \infty )\,.$

Das kommt von der Definitionsmenge $E:=\mathbb {R} ^{2}\!\setminus \!\{(0,0)\}$ der Funktion $\operatorname {arctan2} \,,$ der „gelochten“ Ebene, welche mit einer Gruppenstruktur versehen werden kann, die isomorph ist zur multiplikativen Gruppe $\mathbb {C} ^{\times }$ der komplexen Zahlen ohne die Null. Diese Gruppen sind direktes Produkt der Kreisgruppe $\mathbb S$ der Drehungen und der Gruppe der Streckungen um einen Faktor größer Null, der multiplikativen Gruppe $\mathbb {R} ^{+}.$ Erstere Gruppe lässt sich durch den Polarwinkel $\varphi$ parametrisieren, zweitere durch den (positiven) Betrag $r\ .$

Lösung: Zwei Argumente

Zwei vom Ursprung ${\mathsf {O}}(0,0)$ verschiedene Punkte ${\mathsf {P_{1}}}(x_{1},y_{1})$ und ${\mathsf {P_{2}}}(x_{2},y_{2})$ spezifizieren denselben Polarwinkel, wenn sie auf demselben Strahl durch ${\mathsf {O}}$ liegen. Dann sind sie bezüglich der durch

	$x_{1}\neq 0\;\vee \;y_{1}\neq 0\;:$
	$(x_{1},y_{1})\sim (x_{2},y_{2})$	$:\Longleftrightarrow \;\exists \lambda \;{\color {Red}>}\;0\colon x_{2}=\lambda x_{1}\wedge y_{2}=\lambda y_{1}$

definierten Relation äquivalent.^[1] Dagegen ist der Tangenswert von Polarwinkeln auch dann derselbe, wenn der Strahl um $\pm 180^{\circ }$ oder $\pm \pi$ , also genau in den Gegenstrahl, weitergedreht ist. Informationstheoretisch betrachtet lässt der Tangens die Vorzeicheninformation von $\lambda$ (rot in den Formeln) unter den Tisch fallen:

	$x_{1}\neq 0\;\wedge \;x_{2}\neq 0\;:$
	$\tan \left({\frac {y_{1}}{x_{1}}}\right)=\tan \left({\frac {y_{2}}{x_{2}}}\right)$	$\Longleftrightarrow \;\exists \lambda \;{\color {Red}\gtrless }\;0\colon x_{2}=\lambda x_{1}\wedge y_{2}=\lambda y_{1},$

man nehme nur $\lambda :={\tfrac {x_{2}}{x_{1}}}$ .

Abb. 1: Graph der Arkustangensfunktion

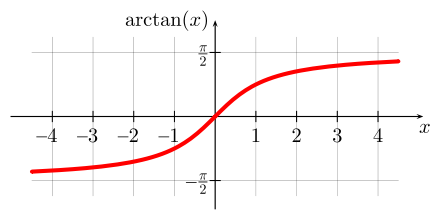
Da der Tangens mit $\pi$ periodisch ist und der Funktionsbegriff Rechtseindeutigkeit verlangt, muss für seine Umkehrung (Spiegelung an der 1. Winkelhalbierenden) sein Definitionsbereich mindestens auf die Periodenlänge eingeschränkt werden – in diesem Artikel auf das Intervall $]-\pi /2,\pi /2[$ (s. Abb. 1). Das hat zur Folge, dass die Umkehrfunktion Arkustangens kein größeres Bild als $]-\pi /2,\pi /2[$ haben kann. Dabei ist die ganze reelle Achse $\mathbb {R}$ als Definitionsbereich des Arkustangens zulässig, weil das Bild des Tangens unter $]-\pi /2,\pi /2[$ gerade $\mathbb {R}$ ist.

Um zu einem vollwertigen Polarwinkel zu kommen, gibt es in vielen Programmiersprachen und Tabellenkalkulationen eine erweiterte Funktion, die mit den beiden kartesischen Koordinaten beschickt wird und damit genügend Information hat, um den Polarwinkel modulo $2\pi \mathbb {Z}$ (bspw. im Intervall $]-\pi ,\pi ]$ wie der Abb. 2) und in allen vier Quadranten zurückgeben zu können.

Implementierungen

Die erste Implementierung war nicht später als im Jahr 1966 in der Programmiersprache Fortran. Heute ist die Funktion auch in anderen Programmiersprachen vorhanden.

Die Funktion hat häufig den Namen $\operatorname{atan2}(y,x)$ , so bei den Programmiersprachen Fortran 77, C, C++, Java, Python, Matlab, R, iWork Numbers, LibreOffice Calc. In vielen dieser Programmiersprachen (nicht bspw. bei LibreOffice Calc) ist die Reihenfolge der Argumente umgekehrt, also die -Koordinate das erste Argument. In Common Lisp, wo optionale Argumente existieren, erlaubt die $\operatorname {atan} (y,x)$ -Funktion, die -Koordinate als optionales zweites Argument zu übergeben, wobei die Standardannahme x=1 ist.

Ein anderer Name ist $\operatorname {arctan2} (x,y)$ , so bei den Tabellenkalkulationen Excel und OpenOffice Calc.

In Mathematica ist eine Funktion $\operatorname {ArcTan} (x,y)$ definiert, bei der das erste Argument weggelassen werden kann.

Zur Beachtung: In diesem Artikel wird die Reihenfolge und der Name $\operatorname {arctan2} (x,y)$ verwendet.

Formel

Die sechs Fälle der Funktionsdefinition

$\operatorname {arctan2} \colon$	$\to$	$]-\pi ,+\pi ]$ oder $[-\pi ,+\pi [$			$({\text{K}}\to {\text{P}}_{2})$
	$\mapsto$	${\begin{cases}\\\\\\\\\\\\\\\\\\\end{cases}}$	$\arctan \left({\tfrac {y}{x}}\right)$	für	(Quadranten $\mathrm{I}$ und $\mathrm {IV}$ )
			$\arctan \left({\tfrac {y}{x}}\right)+\pi$	für $x<0,\ y>0$	(Quadrant $\mathrm {II}$ )
			$\pm \pi$	für $x<0,\ y=0$	(^oberer⁄_unterer Rand der Bildmenge)
			$\arctan \left({\tfrac {y}{x}}\right)-\pi$	für $x<0,\ y<0$	(Quadrant $\mathrm {III}$ )
			$+{\tfrac {\pi }{2}}$	für $x=0,\ y>0$
			$-{\tfrac {\pi }{2}}$	für $x=0,\ y<0$

mit $E:=\mathbb {R} ^{2}\!\setminus \!\{(0,0)\}$ als der „gelochten“ Ebene lassen sich zur Formel

$\operatorname {arctan2} (x,y):=\arctan \left({\tfrac {y}{x}}\right)\operatorname {sgn}(x)^{2}+{\tfrac {1-\operatorname {sgn}(x)}{2}}\left(\mp \operatorname {sgn}(y)^{2}+\operatorname {sgn}(y)\pm 1\right)\pi$

vereinigen. Die Funktion ist bis auf den Fall $x<0,\ y=0\iff (x,y)\sim (-1,0)$ (die Sprungstelle, s.u.) punktsymmetrisch am Ursprung, in Formeln:

$\operatorname {arctan2} (x,-y)=-\operatorname {arctan2} (x,y)$ .

Andererseits ist

$\operatorname {arctan2} (-x,y)={\begin{cases}\\\\\\\end{cases}}$	$-\operatorname {arctan2} (x,y)+\operatorname {sgn}(y)\pi$	für $y\neq 0$
	$0$	für $y=0\wedge x<0$
	$\pm \pi$	für $y=0\wedge x>0$ (die Sprungstelle).

Dem Argument (x,y) = (0,0) wird manchmal der Funktionswert $0$ zugeordnet, wie auch andere Sonderfälle, bspw. Not a Number, unterschiedlich behandelt werden.

Der Genauigkeitsverlust der Division ${\tfrac {y}{x}}$ wegen lässt sich für $0<|x|\ll |y|$ bspw. durch die Umformung

$\arctan \!{\bigl (}{\tfrac {y}{x}}{\bigr )}=-\arctan \!{\bigl (}{\tfrac {x}{y}}{\bigr )}+\operatorname {sgn}(y){\tfrac {\pi }{2}}$

verringern (s. jedoch auch den Abschnitt Genauigkeitskontrolle).

Sprungstelle und kontinuierliche Drehung des Polarwinkels

Abb. 2: Graph von $\operatorname {arctan2} (x|y)$ über $x^{-1}y=y/x$ für $|x|\gg 0$ .
$\operatorname {arctan2}$ -Ziel- =

-Quell-Quadrant mit blauer römischer Ziffer.

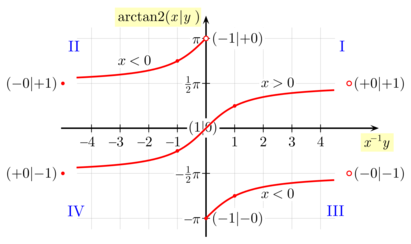
Bei zunehmendem Polarwinkel $\varphi$ , das heißt bei einer Drehung im mathematischen Sinn (und entgegen dem Uhrzeigersinn), beginnt eine Periode in der Abb. 2 unten am (Strahl durch den) Punkt^[8]

$\varphi$			${\tfrac {y}{x}}$
$-\pi$			$0$	${\color {Blue}{\rm {III}}}$	,

von wo es auf dem roten Graphen von links unten nach rechts oben (immer in „ONO-Richtung“) weitergeht. Wie üblich soll in der Nähe der Null infinitesimal unterhalb und infinitesimal oberhalb bedeuten. Die Drehung führt weiter in den Quadranten $\mathrm {III}$ über den (auf der 1. Winkelhalbierenden liegenden und in der Abb. durch eine kleine rote Kreisfläche markierten) Punkt

$-{\tfrac {3\pi }{4}}$

${\color {Blue}{\rm {III}}}$

zum Punkt

	$x_{\color {Red}\bullet }$	$y_{\color {Red}\bullet }$	${\tfrac {y_{\color {Red}\bullet }}{x_{\color {Red}\bullet }}}$	$\varphi$	$x_{\color {Red}{\mathsf {o}}}$	$y_{\color {Red}{\mathsf {o}}}$	${\tfrac {y_{\color {Red}{\mathsf {o}}}}{x_{\color {Red}{\mathsf {o}}}}}$
${\color {Blue}{\rm {IV}}}$			$-\infty$	$-{\tfrac {\pi }{2}}$			$+\infty$	${\color {Blue}{\rm {III}}}$	,

der einer der Polstellen $-{\tfrac {\pi }{2}}$ des Tangens entspricht und deshalb für den Arkustangens $\operatorname {arctan}$ ein unendlich ferner Punkt ist. Der $(x^{-1}y=y/x)$ -Wert wechselt von $+\infty$ nach $-\infty$ . Diesen Sachverhalt symbolisiert die Abb. 2 mit dem roten Kringel rechts im Quadranten $\mathrm {III}$ als Senke und dem roten Punkt links im Quadranten $\mathrm {IV}$ als Quelle. Aus Sicht der Funktion $\operatorname {arctan2} (x|y)$ geschieht aber nichts weiter, als dass der -Wert sich von zu ändert.

Die weitere Drehung führt durch den Quadranten $\mathrm {IV}$ über den markierten Punkt

${\color {Blue}{\rm {IV}}}$

$-{\tfrac {\pi }{4}}$

zum Punkt

${\color {Blue}{\rm {IV}}}$

$0$

${\color {Blue}{\rm {I}}}$

der im Koordinatenursprung liegt, und von dort durch den Quadranten $\mathrm{I}$ über den markierten Punkt

${\tfrac {\pi }{4}}$

${\color {Blue}{\rm {I}}}$

zum Punkt

${\color {Blue}{\rm {II}}}$

$-\infty$

${\tfrac {\pi }{2}}$

$+\infty$

${\color {Blue}{\rm {I}}}$

Dieser Punkt entspricht der anderen Polstelle $+{\tfrac {\pi }{2}}$ des Tangens. Bei ihm findet dasselbe Zusammenfallen der Senke im Quadranten $\mathrm{I}$ mit der Quelle im Quadranten $\mathrm {II}$ statt wie oben beim Argument $(0\,|\!-\!1)$ . Die weitere Drehung durch den Quadranten $\mathrm {II}$ führt über den markierten Punkt

${\color {Blue}{\rm {II}}}$

${\tfrac {3\pi }{4}}$

schließlich zur Sprungstelle

${\color {Blue}{\rm {II}}}$

$0$

$\pi$

Dieser Fall kann durch leichte Abwandlung der Bedingungen in der Formel $({\text{K}}\to {\text{P}}_{2})$ entweder dem Fall in der Zeile darüber oder dem darunter zugeschlagen werden, wonach das Intervall der Bildmenge an seinem oberen Ende abgeschlossen und am unteren Ende offen ist, also $]-\pi ,+\pi ]$ , oder eben umgekehrt $[-\pi ,+\pi [$ .

Hat die Berechnung des Polarwinkels eine kontinuierliche Drehung zu begleiten, dann kann die Funktion so angepasst oder erweitert werden, dass

die Sprungstelle an einem beliebigen Punkt (einem beliebigen Strahl) des Definitionsbereichs $\mathbb {R} ^{2}\!\setminus \!\{(0|0)\}$ liegt;
auch bei einer Drehung über die Periodenlänge $2\pi$ hinaus der Polarwinkel kontinuierlich zu- bzw. abnimmt. Hier kommt die Umlaufzahl ins Spiel.

Beispielsweise können in Anwendungen, bei denen es auf die Stetigkeit innerhalb einer Halbebene ankommt, folgende Formeln nützlich sein:

$\operatorname {arctan2} _{-3}(x\|y):=-$	$\arctan {\bigl (}{\tfrac {x}{y}}{\bigr )}-{\tfrac {3\pi }{2}}$	$=\operatorname {arctan2} (x\|y)-2\pi$	für	(Quadranten ${\color {Blue}{\rm {I}}}$ und ${\color {Blue}{\rm {II}}}$ )
$\operatorname {arctan2} _{-2}(x\|y):=$	$\arctan \left({\tfrac {y}{x}}\right)-\pi$	$\equiv \operatorname {arctan2} (x\|y){\text{ mod }}2\pi \mathbb {Z}$	für	(Quadranten ${\color {Blue}{\rm {II}}}$ und ${\color {Blue}{\rm {III}}}$ )
$\operatorname {arctan2} _{-1}(x\|y):=-$	$\arctan {\bigl (}{\tfrac {x}{y}}{\bigr )}-{\tfrac {\pi }{2}}$	$\left.{\begin{matrix}\\\\\\\\\end{matrix}}\right\rbrace =\operatorname {arctan2} (x\|y)\qquad \qquad \left\lbrace {\begin{matrix}\\\\\\\\\end{matrix}}\right.$	für $y<0$	(Quadranten ${\color {Blue}{\rm {III}}}$ und ${\color {Blue}{\rm {IV}}}$ )
$\operatorname {arctan2} _{\,0\,}(x\|y):=$	$\arctan \left({\tfrac {y}{x}}\right)$		für	(Quadranten ${\color {Blue}{\rm {IV}}}$ und ${\color {Blue}{\rm {I}}}$ )
$\operatorname {arctan2} _{+1}(x\|y):=-$	$\arctan {\bigl (}{\tfrac {x}{y}}{\bigr )}+{\tfrac {\pi }{2}}$		für	(Quadranten ${\color {Blue}{\rm {I}}}$ und ${\color {Blue}{\rm {II}}}$ )
$\operatorname {arctan2} _{+2}(x\|y)=$	$\arctan \left({\tfrac {y}{x}}\right)+\pi$	$\equiv \operatorname {arctan2} (x\|y){\text{ mod }}2\pi \mathbb {Z}$	für	(Quadranten ${\color {Blue}{\rm {II}}}$ und ${\color {Blue}{\rm {III}}}$ )
$\operatorname {arctan2} _{+3}(x\|y):=-$	$\arctan {\bigl (}{\tfrac {x}{y}}{\bigr )}+{\tfrac {3\pi }{2}}$	$=\operatorname {arctan2} (x\|y)+2\pi$	für $y<0$	(Quadranten ${\color {Blue}{\rm {III}}}$ und ${\color {Blue}{\rm {IV}}}$ )

Die 7 Zeilen sind so angeordnet, dass die Werte zweier über einander stehender Funktionen im gemeinsamen Definitionsgebiet übereinstimmen. Wegen der Sprungstelle von $\operatorname {arctan2} (x|y)$ beim Strahl $\sim (\!-1|0)$ ist Gleichheit mit einer der stetigen Funktionen $\operatorname {arctan2} _{\mp 2}(x|y)$ nicht möglich.

Isomorphie zur Kreisgruppe

Die präzise mathematische Darstellung der folgenden wohlbekannten Abbildung bedarf sowohl auf der Urbild- wie auf der Bild-Seite zusätzlicher Hilfsabbildungen.

Auf der Definitionsmenge $E:=\mathbb {R} ^{2}\!\setminus \!\{(0,0)\}$ von $\operatorname {arctan2}$ kann man (in Analogie zur Definition der Addition in den rationalen Zahlen) die Verknüpfung

$(x,y){\tilde {+}}(x',y'):=(xx'-yy',xy'+yx')$

definieren.^[3] Sie bleibt wohldefiniert unter der obigen Äquivalenzrelation $\sim$ , und die Faktormenge

$F:=E/\sim$

erweist sich als kommutative Gruppe mit dem neutralen Element ${\overline {(1,0)}}$ und der Inversenbildung

${\tilde {-}}{\overline {(x,y)}}:={\overline {(x,-y)}}$ .^[4]

Genauso wohldefiniert ist die induzierte Abbildung

${\begin{array}{rlll}\operatorname {arctan2} \;\colon &F&\to &]-\pi ,+\pi ]\\&{\overline {(x,y)}}&\mapsto &\operatorname {arctan2} (x,y)\end{array}}$

weil äquivalente Repräsentanten denselben $\operatorname {arctan2}$ -Wert liefern. Aus der Summenformel des Arkustangens folgt

${\begin{array}{rlll}\operatorname {arctan2} \left((x,y){\tilde {+}}(x',y')\right)&\equiv \operatorname {arctan2} (xx'-yy',xy'+yx')\\&\equiv \operatorname {arctan2} (x,y)+\operatorname {arctan2} (x',y')\quad {\bmod {\,}}2\pi \mathbb {Z} .\end{array}}$

Wendet man auf die Funktion $\operatorname {arctan2}$ die Funktion

${\begin{array}{rlll}\operatorname {mod} \!2\pi \;\colon &]-\pi ,+\pi ]\;\;&\to &\mathbb {R} /(2\pi \mathbb {Z} )\\&\varphi &\mapsto &\varphi +2\pi \mathbb {Z} \end{array}}$

an, dann ergibt sich ein Homomorphismus $\mu :=\operatorname {mod} \!2\pi \circ \operatorname {arctan2}$ mit

${\begin{array}{rlll}\mu \;\colon &F&\to &\mathbb {R} /(2\pi \mathbb {Z} )&&\cong \mathbb {S} \\&{\overline {(x,y)}}\;{\tilde {+}}\;{\overline {(x',y')}}&\mapsto &\mu (x,y)+\mu (x',y')\end{array}}$

auf die Kreisgruppe $\mathbb S$ , dessen Kern das neutrale Element ${\overline {(1,0)}}$ mit $\mu {\overline {(1,0)}}=2\pi \mathbb {Z}$ ist. Sind und $\mathbb {R} /(2\pi \mathbb {Z} )$ mit der natürlichen Topologie ausgestattet, dann ist $\mu$ in beiden Richtungen stetig, mithin ein Homöomorphismus.

Genauigkeitskontrolle

Mit einer kleinen Vorbereitung und mit nur einem Vergleich mehr als in den Fallunterscheidungen der Formel $({\text{K}}\to {\text{P}}_{2})$ lässt sich das Konvergenzverhalten der Taylorreihe (des Arkustangens) kontrollieren und ggf. verbessern.

Der Winkel von $45^{\circ }$ zeichnet sich dadurch aus, dass er ein ganzzahliger Bruchteil, nämlich ein Achtel, des vollen Winkels von $360^{\circ }$ ist und gleichzeitig sein Strahl durch ganzzahlige Koordinaten geht. Quadranten lassen sich in der Koordinatenebene so ausrichten, dass ihre Begrenzungen (die definitionsgemäß stets Strahlen sind) parallel zu den Koordinatenachsen zu liegen kommen. Bei Oktanten^[5] kommen noch die Winkelhalbierenden als Begrenzungen hinzu. Die Feststellung, zu welchem der acht Oktanten ein Punkt $(x,y)\in E$ gehört, ist bei einer derartigen Ausrichtung besonders einfach.

Schreibweise: In diesem Abschnitt werden in den Beziehungen zwischen Strahlen und Winkeln die gewohnten Operatoren $+\;-\;=\;<\;>$ mit der darübergeschriebenen Tilde ${\tilde {+}}\;{\tilde {-}}\;{\tilde {=}}\;{\tilde {<}}\;{\tilde {>}}$ verwendet, um auszudrücken, dass ein Strahl eine Äquivalenzklasse ${\text{mod }}\sim$ ist. Und bei den Vergleichsoperatoren ${\tilde {<}}\;{\tilde {>}}$ wird der Strahl stets mit dem ihm ${\text{mod }}2\pi \mathbb {Z}$ am nächsten liegenden Winkel verglichen.; Um Verwechslungen mit Koordinaten zu vermeiden, wird in den Dezimaldarstellungen statt des Kommas der Dezimalpunkt verwendet.

Im Folgenden wird versucht, einen beliebigen Strahl (x,y) resp. Winkel $\varphi$ mit einfachen und umkehrbaren Drehungen in das an der Polarachse symmetrische Winkelintervall $-22.5^{\circ }\leq \varphi _{2}\leq 22.5^{\circ }$ zu drehen. Dann ist nämlich der Absolutbetrag des Arguments ${\tfrac {y_{2}}{x_{2}}}$ in der Taylorreihe des Arkustangens $\left|{\tfrac {y_{2}}{x_{2}}}\right|\;\leq \;\tan 22.5^{\circ }$ $={\sqrt {2}}-1\approx 0.41421$ .

In einer ersten Drehung wird der Strahl $(x,y)\in E$ um $-22.5^{\circ }$ gedreht, d.h. der Strahl

$(x_{0},y_{0}):=(x,y)\;{\tilde {-}}\;(1,{\sqrt {2}}-1)=(x,y)\;{\tilde {-}}\;22.5^{\circ }$

gebildet. Der Oktant, in den dieser Strahl fällt, sei der -te, und die Nummerierung der Oktanten sei so gewählt, dass der erste das Winkelintervall $]0^{\circ },45^{\circ }]$ abdeckt:

Nummer des Oktanten
seine untere und obere Begrenzung

$\displaystyle -180\overbrace {\displaystyle ^{\circ }\,-\!13} ^{\displaystyle -3}5\overbrace {\displaystyle ^{\circ }\;\;-\!9} ^{\displaystyle -2}0\overbrace {\displaystyle ^{\circ }\;\,\ -\!4} ^{\displaystyle -1}5\overbrace {\displaystyle ^{\circ }\quad \;\;\;\;} ^{\displaystyle 0}0\overbrace {\displaystyle ^{\circ }\quad \,\,\,\ 4} ^{\displaystyle 1}5\overbrace {\displaystyle ^{\circ }\quad \;\;9} ^{\displaystyle 2}0\overbrace {\displaystyle ^{\circ }\quad \,13} ^{\displaystyle 3}5\overbrace {\displaystyle ^{\circ }\quad \,18} ^{\displaystyle 4}\displaystyle 0^{\circ }$

die obere als Strahl $(x_{1},y_{1})={\big [}{\begin{smallmatrix}x_{1}\\y_{1}\end{smallmatrix}}{\big ]}$

$\in$

${\Big \{}$

${\big [}{\begin{smallmatrix}-1\\-1\end{smallmatrix}}{\big ]}$

$,\;{\big [}{\begin{smallmatrix}0\\-1\end{smallmatrix}}{\big ]}$

$,\;{\big [}{\begin{smallmatrix}+1\\-1\end{smallmatrix}}{\big ]}$

$,\;{\big [}{\begin{smallmatrix}+1\\0\end{smallmatrix}}{\big ]}$

$,\;{\big [}{\begin{smallmatrix}+1\\+1\end{smallmatrix}}{\big ]}$

$,\;{\big [}{\begin{smallmatrix}0\\+1\end{smallmatrix}}{\big ]}$

$,\;{\big [}{\begin{smallmatrix}-1\\+1\end{smallmatrix}}{\big ]}$

$,\;{\big [}{\begin{smallmatrix}-1\\0\end{smallmatrix}}{\big ]}$

${\Big \}}$

die obere als Polarwinkel $\varphi_1$

$-{\tfrac {3\pi }{4}}$

$-\tfrac{\pi}{2}$

$-{\tfrac {\pi }{4}}$

$0$

$\tfrac{\pi}{4}$

${\tfrac {\pi }{2}}$

${\tfrac {3\pi }{4}}$

$\pm \pi$

Vom derart bestimmten Oktanten wird der obere begrenzende Strahl genommen, der durch einen Punkt $(x_{1},y_{1})\in E$ aus der in der Tabelle gezeigten Menge von Strahlen charakterisiert werden kann. (Alle diese Punkte haben ganzzahlige Koordinaten, und beim ersten Oktanten ist bspw. $(x_{1},y_{1})\;{\tilde {=}}\;(+1,+1)\;{\tilde {=}}\;45^{\circ }$ .) Dann ist $(x_{1},y_{1})\;{\tilde {-}}\;45^{\circ }\;{\tilde {\leq }}\;(x_{0},y_{0})\;{\tilde {\leq }}\;(x_{1},y_{1})$ oder

$(x_{1},y_{1})\;{\tilde {-}}\;22.5^{\circ }\quad {\tilde {\leq }}\quad (x_{0},y_{0})\;{\tilde {+}}\;22.5^{\circ }=(x,y)\quad {\tilde {\leq }}\quad (x_{1},y_{1})\;{\tilde {+}}\;22.5^{\circ }$ .

Es folgt eine Drehung von (x,y) , die zweite, jetzt um ${\tilde {-}}(x_{1},y_{1})$ , so dass

$-22.5^{\circ }\quad {\tilde {\leq }}\quad (x_{2},y_{2}):=(x,y)\;{\tilde {-}}\;(x_{1},y_{1})\quad {\tilde {\leq }}\quad +22.5^{\circ }$

im gewünschten Winkelintervall ist. Um diese zweite Drehung von $\varphi _{1}:=\operatorname {arctan2} (x_{1},y_{1})$ $=k\cdot 45^{\circ }=k\cdot {\tfrac {\pi }{4}}$ mit ganzzahligem muss das Ergebnis, wenn der Arkustangens berechnet ist, korrigiert werden.

Die erste Drehung muss nur ungefähr $22.5^{\circ }$ betragen. Wenn sie davon etwas abweicht, etwa $(5,2)\;{\tilde {=}}\;21.8^{\circ }$ oder auch $(70,29)\;{\tilde {=}}\;22.5035^{\circ }$ beträgt, dann wird der Strahl (x_2, y_2) möglicherweise nicht so gut in das an der Polarachse symmetrische Winkelintervall eingepasst. Das Konvergenzverhalten verschlechtert sich aber wegen $(1,1){\tilde {+}}(5,-2)\;{\tilde {=}}\;(7,3)$ nur geringfügig auf $\left|{\tfrac {y_{2}}{x_{2}}}\right|\leq \max \left\{\left|{\tfrac {-2}{5}}\right|;\left|{\tfrac {3}{7}}\right|\right\}={\tfrac {3}{7}}\approx 0.42857$ .

Nach der zweiten Drehung kann die Taylorreihe (an der Entwicklungsstelle $0$ )

$\varphi _{2}:=\operatorname {arctan2} (x_{2},y_{2})=\arctan \left({\tfrac {y_{2}}{x_{2}}}\right)$

entwickelt und die abschließende Korrektur

$\varphi :=\varphi _{2}+\varphi _{1}=\operatorname {arctan2} (x,y)$

vorgenommen werden.

Beispiele

Der Ausgangsstrahl sei $(x,y):=(-5,27)$ , was einem Winkel von ca. $100^\circ$ entspricht. Durch die ${\tilde {+}}$ -Addition von $(5,-2)$ kommen wir auf $(x_{0},y_{0})=(1,5)\;{\tilde {=}}\;79^{\circ }$ , also in den -ten Oktanten. Dessen obere Begrenzung liegt bei $\varphi _{1}:=2\cdot 45^{\circ }=+{\tfrac {\pi }{2}}\;{\tilde {=}}\;(0,1)=:(x_{1},y_{1})$ . Wir bilden die Differenz $(x_{2},y_{2}):=(x,y)\;{\tilde {-}}\;(x_{1},y_{1})=(-5,27)\;{\tilde {-}}\;(0,1)=(27,5)$ und berechnen $\varphi _{2}=\operatorname {arctan2} (27,5)=\arctan \left({\tfrac {5}{27}}\right)\approx 10^{\circ }$ mit ${\tfrac {5}{27}}\approx 0.185$ und korrigieren mit $\varphi _{1}=+{\tfrac {\pi }{2}}$ zum Endergebnis $\varphi \approx 100^{\circ }$ .
Der Ausgangsstrahl sei $(-19,-4)$ , was einem Winkel von ca. $-168^{\circ }$ entspricht. Durch die ${\tilde {+}}$ -Addition von $(5,-2)$ kommen wir auf $(-103,18){\tilde {=}}170^{\circ }$ , also in den -ten Oktanten. Das obere Ende des Oktanten liegt bei $\varphi _{1}:=4\cdot 45^{\circ }=\pi \;{\tilde {=}}\;(-1,0)=:(x_{1},y_{1})$ . Da dieser Oktant die Sprungstelle enthält, setzen wir bei diesem -ten Oktanten im Fall den Korrekturwinkel auf $\varphi _{1}:=-\pi$ . Wir bilden die Differenz $(-19,-4){\tilde {-}}(-1,0)=(19,4)$ und berechnen $\operatorname {arctan2} (19,4)=\arctan \left(\displaystyle {\tfrac {4}{19}}\right)$ mit $\displaystyle {\tfrac {4}{19}}\approx 0.211$ und korrigieren mit $\varphi_1$ .

Verbindung zum komplexen Logarithmus

Man kann die Funktion $\operatorname {arctan2} (x,y)$ für $(x,y)\in E\cong \mathbb {C} ^{\times }$ auch über den Hauptwert $\ln$ des komplexen Logarithmus definieren als

$\operatorname {arctan2} (x,y):=\arg(x+\mathrm {i} \,y)=\operatorname {Im} \,\ln(x+\mathrm {i} \,y)={\frac {1}{\mathrm {i} }}\ln {\frac {x+\mathrm {i} \,y}{\sqrt {x^{2}+y^{2}}}}$

mit der Argument-Funktion $\arg$ . Diese Funktion wird zum Beispiel in der inversen Kinematik benutzt, um Gelenkeinstellungen korrekt zu beschreiben. Dies ist allerdings nur eine andere formale Darstellung, denn zur Berechnung muss man $\ln z$ mit |z|=1 bestimmen und dazu die gegebene kartesische Darstellung von $z=:x+\mathrm {i} \,y$ in die Polarform überführen, wobei man im Endeffekt wieder auf die oben definierte $\operatorname {arctan2}$ -Funktion mit reellen Argumenten zurückgreift.

Ableitungen

Die Funktion $\operatorname {arctan2}$ hängt von zwei Variablen ab und ist (außer im Ursprung) stetig differenzierbar, hat also zwei partielle Ableitungen. Für die Bedingung des ersten Falls und dessen Zuordnung ergibt sich

${\begin{aligned}{\frac {\partial }{\partial x}}\operatorname {arctan2} (x,y)&={\frac {\partial }{\partial x}}\arctan \left({\frac {y}{x}}\right)={\frac {-y}{x^{2}+y^{2}}},\\{\frac {\partial }{\partial y}}\operatorname {arctan2} (x,y)&={\frac {\partial }{\partial y}}\arctan \left({\frac {y}{x}}\right)={\frac {x}{x^{2}+y^{2}}}.\end{aligned}}$

Die Einschränkung auf den ersten Fall kann nachträglich fallen gelassen werden, so dass die Gleichungen für alle $(x,y)\in E$ gelten.^[12]

Damit ist

$\operatorname {grad} \operatorname {arctan2} (x,y)=\nabla \operatorname {arctan2} (x,y)=\left({\frac {-y}{x^{2}+y^{2}}},{\frac {x}{x^{2}+y^{2}}}\right)$

der Gradient der Funktion $\operatorname {arctan2}$ , und seine Richtung ist an jedem Punkt (x,y) senkrecht zum Radiusvektor in mathematisch positiver Drehrichtung. Das passt zu der Tatsache, dass der Funktionswert von $\operatorname {arctan2}$ , der Polarwinkel, in dieser Richtung zunimmt.

Des Weiteren folgt für das totale Differential

$\mathrm {d} \operatorname {arctan2} ={\frac {\partial \operatorname {arctan2} }{\partial x}}\,\mathrm {d} x+{\frac {\partial \operatorname {arctan2} }{\partial y}}\,\mathrm {d} y={\frac {-y}{x^{2}+y^{2}}}\mathrm {d} x+{\frac {x}{x^{2}+y^{2}}}\mathrm {d} y\,.$

Eine Integration dieses Differentials entlang eines Weges ergibt die Änderung des (Polar)winkels über den Weg. Ist der Weg geschlossen, so erhält man die Umlaufzahl (in Bezug auf den Ursprung (0,0) ).

Siehe auch

Anmerkungen

↑ Die Begriffsbildung gestattet u.a. eine einfachere und präzisere Spezifikation der Werte $+\infty \;:\sim \;(0,+1)$ und $-\infty :\sim (0,-1),$ die der auf zwei Tangens-Perioden aufgeteilten Polstelle des Tangens entsprechen.
↑ Entsprechend den 2 Argumenten der $\operatorname {arctan2}$ -Funktion werden zwei Koordinaten als unabhängige Variable und nicht nur der Quotient aufgeführt.
↑ Diese Definition stimmt überein mit den Regeln der komplexen Multiplikation, welche auch dem Additionstheorem des Tangens zugrunde liegen.
In diesem Artikel kommt es besonders auf ihre Eignung für ganzzahlige Koordinaten an.
↑ Von den komplexen Zahlen her weiß man, dass das ${\tilde {+}}$ -Inverse von auf ganz (und nicht nur auf )

$\left({\frac {x}{x^{2}+y^{2}}},{\frac {-y}{x^{2}+y^{2}}}\right)$
ist und dass $(E,{\tilde {+}})\cong (\mathbb {C} ^{\times },\cdot )$ eine abelsche Gruppe ist, was aber im Text so nicht gebraucht wird.
↑ Gemeint ist der Halbquadrant, der dem nautischen Gerät Oktant und der Windrose mit den vier Nebenhimmelsrichtungen entspricht, und nicht der dreidimensionale Oktant (Geometrie).
↑ Die Ableitungen sind gebrochen rationale Funktionen und enthalten keine transzendente Funktion. Dieses Phänomen ist aber schon vom Arkustangens her bekannt.

Basierend auf einem Artikel in:

Wikipedia.de