
Polynom
Ein Polynom summiert die Vielfachen von Potenzen einer Variablen bzw. Unbestimmten:
oder kurz mit dem Summenzeichen:
Dabei ist
das Summenzeichen, die Zahlen
sind die jeweiligen Vielfachen und
ist die Unbestimmte.
Exponenten der Potenzen sind natürliche Zahlen. Die Summe ist außerdem stets endlich. Unendliche Summen von Vielfachen von Potenzen mit natürlichzahligen Exponenten einer Unbestimmten heißen formale Potenzreihen.
In der elementaren
Algebra identifiziert man diesen Ausdruck mit einer Funktion in
(einer Polynomfunktion).
In der abstrakten Algebra unterscheidet man streng zwischen einer
Polynomfunktion und einem Polynom als Element eines Polynomrings.
In der Schulmathematik wird eine Polynomfunktion oft auch als ganzrationale
Funktion bezeichnet.
Dieser Artikel erklärt außerdem die mathematischen Begriffe: Leitkoeffizient, Normieren eines Polynoms und Absolutglied.
Etymologie
Das Wort Polynom bedeutet so viel wie „mehrnamig“. Es entstammt dem
griech. πολύ polý „viel“ und όνομα onoma „Name“. Diese Bezeichnung
geht zurück bis auf Euklids
Elemente. In Buch X nennt er eine zweigliedrige Summe
ἐκ δύο ὀνομάτων (ek dýo onomátōn): „aus zwei Namen (bestehend)“. Die Bezeichnung
Polynom geht auf Viëta
zurück: In seiner Isagoge (1591) verwendet er den Ausdruck polynomia
magnitudo für eine mehrgliedrige Größe.
Polynome in der elementaren Algebra
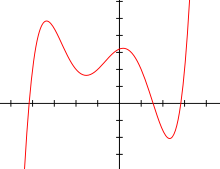
Im Gegensatz zur abstrakten Algebra werden Polynome in der elementaren Algebra als Funktionen aufgefasst. Daher wird in diesem Abschnitt der Begriff Polynomfunktion anstatt Polynom verwendet.
Definition
In der elementaren
Algebra ist eine Polynomfunktion eine Funktion
der Form
,
wobei als Definitionsbereich
für die (unabhängige)
Variable
jede beliebige
-Algebra
in Frage kommt, wenn
der Wertebereich der Koeffizienten ist (siehe unten). Häufig ist dieser jedoch
die Menge der ganzen,
der reellen
oder der komplexen
Zahlen. Die
stammen aus einem Ring
,
zum Beispiel einem Körper
oder einem Restklassenring,
und werden Koeffizienten
genannt.
- Alle Exponenten sind natürliche Zahlen.
- Als Grad
des Polynoms wird der höchste Exponent
bezeichnet, für den der Koeffizient
des Monoms
nicht null ist. Dieser Koeffizient heißt Leitkoeffizient (auch: führender Koeffizient). (Die Schreibweise
für den Grad des Polynoms
ist vom englischen Begriff degree abgeleitet. In der deutschsprachigen Literatur findet sich häufig auch die aus dem Deutschen kommende Schreibweise
oder
.)
- Die Menge aller reellen Polynomfunktionen beliebigen (aber endlichen) Grades ist ein Vektorraum, der sich nicht offensichtlich mittels geometrischer Vorstellungen veranschaulichen lässt.
- Für das Nullpolynom, bei dem alle
Null sind, wird der Grad als
definiert.
- Ist der Leitkoeffizient 1, dann heißt das Polynom normiert oder auch monisch.
- Sind die Koeffizienten teilerfremd, bzw. ist der Inhalt 1, dann heißt das Polynom primitiv.
Der Koeffizient
heißt Absolutglied.
wird als lineares Glied bezeichnet,
als quadratisches Glied und
als kubisches.
Einfaches Beispiel
Durch
ist ein Polynom dritten Grades gegeben (der höchste vorkommende Exponent ist
3). In diesem Beispiel ist 9 der Leitkoeffizient (als Faktor vor
der höchsten Potenz von ),
die weiteren Koeffizienten lauten: 1; 7 und −3,8.
Bezeichnung spezieller Polynomfunktionen
Polynome des Grades
- 0 werden konstante
Funktionen genannt (z.B.
).
- 1 werden lineare
Funktionen oder genauer affin lineare Funktionen genannt
(z.B.
).
- 2 werden quadratische
Funktionen genannt (z.B.
).
- 3 werden kubische
Funktionen genannt (z.B.
).
- 4 werden quartische
Funktionen genannt (z.B.
).
Nullstellen
Als Nullstellen einer
Polynomfunktion oder Wurzeln bzw. Lösungen
einer Polynomgleichung werden jene Werte von
bezeichnet, für die der Funktionswert
null ist, das heißt, die die Gleichung
erfüllen. Eine Polynomfunktion über einem Körper (oder allgemeiner einem Integritätsring)
hat stets höchstens so viele Nullstellen, wie sein Grad angibt.
Weiterhin besagt der Fundamentalsatz
der Algebra, dass eine komplexe Polynomfunktion (das heißt eine
Polynomfunktion mit komplexen
Koeffizienten) vom Grad
mindestens eine komplexe
Nullstelle hat (reiner Existenzsatz). Dann gibt es genau
Nullstellen (Polynomdivision),
wenn die Nullstellen entsprechend ihrer Vielfachheit gezählt werden. So
ist beispielsweise die Nullstelle
der Polynomfunktion
eine doppelte. Im Ergebnis lässt sich jede komplexe Polynomfunktion
positiven Grades in ein Produkt
von Linearfaktoren
zerlegen. Allgemein kann man zu jedem Körper
eine algebraische
Körpererweiterung
finden, in der alle Polynome positiven Grades mit Koeffizienten in
als Polynome über
in Linearfaktoren zerfallen. In diesem Fall nennt man
den algebraischen
Abschluss von
.
Die Nullstellen von Polynomen ersten, zweiten, dritten und vierten Grades lassen sich mit Formeln exakt berechnen (zum Beispiel durch die pq-Formel für quadratische Gleichungen), dagegen lassen sich Polynomfunktionen höheren Grades nur in Spezialfällen mit Hilfe von Wurzelzeichen exakt faktorisieren. Dies ist die Aussage der Satzes von Abel-Ruffini.
Polynome in der abstrakten Algebra
Definition
In der abstrakten
Algebra definiert man ein Polynom als ein Element eines Polynomringes .
Dieser wiederum ist die Erweiterung
des Koeffizientenringes
durch ein unbestimmtes, (algebraisch) freies Element
.
Damit enthält
die Potenzen
,
und deren Linearkombinationen
mit
.
Dies sind auch schon alle Elemente, d.h., jedes Polynom ist eindeutig
durch die Folge
seiner Koeffizienten charakterisiert.
Konstruktion
Umgekehrt kann ein Modell des Polynomrings
durch die Menge der endlichen Folgen in
konstruiert werden. Dazu wird auf
eine Addition „
“
als gliedweise Summe der Folgen und eine Multiplikation „
“
durch Faltung der Folgen definiert. Ist also
und
,
so ist
und
mit diesen Verknüpfungen ist nun selbst ein kommutativer Ring, der Polynomring (in einer
Unbestimmten) über
.
Identifiziert man die Unbestimmte als Folge ,
so dass
,
etc., so kann jede Folge
wieder im intuitiven Sinne als Polynom dargestellt werden als
Zusammenhang mit der analytischen Definition
Bedenkt man nun, dass nach der Voraussetzung eine natürliche Zahl
existiert, so dass
für alle
gilt, so lässt sich nach den obigen Überlegungen jedes Polynom
über einem kommutativen unitären Ring eindeutig schreiben als
.
Dabei ist
jedoch keine Funktion wie in der Analysis oder elementaren Algebra, sondern eine
unendliche Folge (ein Element des Ringes
)
und
ist keine „Unbekannte“, sondern die Folge
.
Man kann jedoch
als „Muster“ benutzen, um danach eine Polynomfunktion (d.h. ein Polynom im
gewöhnlichen analytischen Sinne) zu bilden. Dazu benutzt man den sogenannten
Einsetzungshomomorphismus.
Man sollte allerdings beachten, dass verschiedene Polynome dieselbe
Polynomfunktion induzieren können. Ist beispielsweise
der Restklassenring
,
so induzieren die Polynome
und
- das Nullpolynom
beide die Nullabbildung
,
das heißt:
für alle
Für Polynome über den reellen oder ganzen Zahlen oder allgemein jedem unendlichen Integritätsring ist ein Polynom jedoch durch die induzierte Polynomfunktion bestimmt.
Auch die Menge der Polynomfunktionen mit Werten in
bildet einen Ring (Unterring
des Funktionenrings),
der jedoch nur selten betrachtet wird. Es gibt einen natürlichen Ring-Homomorphismus von
in den Ring der Polynomfunktionen, dessen Kern
die Menge der Polynome ist, die die Nullfunktion induzieren.
Verallgemeinerungen
Polynome in mehreren Unbestimmten
Allgemein versteht man jede Summe von Monomen
der Form
als Polynom (in mehreren Unbestimmten):
- Lies: „Groß-p von Groß-x-1 bis Groß-x-n (ist) gleich die Summe über alle i-1 bis i-n von a-i-1-bis-i-n mal Groß-x-1 hoch i-1 bis Groß-x-n hoch i-n“
Durch eine Monomordnung ist es möglich die Monome in einem solchen Polynom anzuordnen und dadurch Begriffe wie Leitkoeffizient zu verallgemeinern.
Die Größe
heißt der Totalgrad eines Monoms
.
Haben alle (nichtverschwindenden) Monome in einem Polynom denselben Totalgrad,
so heißt es homogen.
Der maximale Totalgrad aller nichtverschwindenden Monome ist der Grad des
Polynoms.
Die maximale Anzahl der möglichen Monome eines bestimmten Grades ist
- Lies: „n+k-1 über k“ oder „k aus n+k-1“
wobei
die Anzahl der vorkommenden Unbestimmten und
der Grad ist. Anschaulich wird hier ein Problem von Kombinationen mit
Wiederholung (Zurücklegen) betrachtet.
Summiert man die Anzahl der möglichen Monome des Grades
bis
,
erhält man für die Anzahl der möglichen Monome in einem Polynom bestimmten
Grades:
- Lies: „n+k über k“ oder „k aus n+k“
Sind alle Unbestimmten in gewisser Weise „gleichberechtigt“, so heißt das Polynom symmetrisch. Gemeint ist: wenn das Polynom sich bei Vertauschungen der Unbestimmten nicht ändert.
Auch die Polynome in den
Unbestimmten
über
dem Ring
bilden einen Polynomring, geschrieben als
.
Formale Potenzreihen
Geht man zu unendlichen Reihen der Form
- Lies: „f (ist) gleich die Summe von i gleich Null bis Unendlich von a-i (mal) (Groß-) x hoch i“
über, erhält man formale Potenzreihen.
Laurent-Polynome und Laurent-Reihen
Lässt man auch in einem Polynom auch negative Exponenten zu, so erhält man ein Laurent-Polynom. Entsprechend zu den formalen Potenzreihen können auch formale Laurent-Reihen betrachtet werden. Es handelt sich dabei um Objekte der Form
Lies: „f (ist) gleich die Summe von i gleich minus (Groß-) n bis Unendlich von a−i (mal) (Groß-) x hoch i“
Posynomialfunktionen
Lässt man mehrere Variablen und beliebige reelle Potenzen zu, so erhält man den Begriff der Posynomialfunktion.
Literatur
- Albrecht Beutelspacher: Lineare Algebra. 8. Auflage, ISBN 978-3-658-02413-0.
- Gerd Fischer: Lehrbuch der Algebra, ISBN 978-3-658-02221-1.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 24.09. 2022