Drehgruppe
Die Drehgruppe im engeren Sinn ist die spezielle
orthogonale Gruppe
oder auch
aller Drehungen im reellen dreidimensionalen Raum (falls
)
oder in der reellen Ebene (falls
),
in letzterem Fall heißt sie Kreisgruppe.
Ihre Elemente sind die Drehmatrizen,
also orthogonale
Matrizen mit Determinante
eins.
Daneben wird eine Untergruppe
dieser reellen Gruppen als Drehgruppe einer zwei- oder dreidimensionalen
Figur bezeichnet, wenn sie alle Drehungen umfasst, die die Figur auf sich
selbst abbilden, also die Untergruppe der Drehungen in der Symmetriegruppe des
Körpers bzw. der Figur ist. Zur Unterscheidung wird die
die volle
-dimensionale
Drehgruppe genannt.
Im weiteren und übertragenen Sinn werden die speziellen orthogonalen Gruppen
– das sind die Untergruppen der reellen
allgemeinen linearen Gruppe ,
deren Elemente orthogonale Matrizen mit Determinante eins sind – auch für höhere
Dimensionen
mit
als (volle) Drehgruppen bezeichnet.
Definition und Eigenschaften
Die orthogonale
Gruppe
ist die Gruppe
der orthogonalen
-Matrizen
mit reellen Elementen. Die Verknüpfung
der orthogonalen Gruppe ist die Matrizenmultiplikation.
Bei der orthogonalen Gruppe handelt es sich um eine Lie-Gruppe
der Dimension
.
Da die Determinante
einer orthogonalen Matrix nur die Werte
annehmen kann, zerfällt
in zwei disjunkte Teilmengen
(topologisch: Zusammenhangskomponenten):
- die Drehgruppe
aller Drehungen (orthogonale Matrizen mit Determinante
) und
- die Menge
aller Drehspiegelungen (orthogonale Matrizen mit Determinante
).
Die Untergruppe
heißt die spezielle orthogonale Gruppe oder die Drehgruppe.
Insbesondere ist die
als die Gruppe aller Drehungen um eine durch den Koordinatenursprung verlaufende
Achse im dreidimensionalen Raum von großer Bedeutung in zahlreichen Anwendungen,
wie etwa der Computergraphik oder der Physik.
Zweidimensionale Drehungen
Die Kreisgruppe
ist die Lie-Gruppe, die die Drehungen um einen festen Punkt im zweidimensionalen
Raum (einer Ebene) zusammenfasst und die Hintereinanderausführung dieser
Drehungen beschreibt. Eine solche Drehung lässt sich eindeutig durch einen
Winkel beschreiben, die Hintereinanderausführung zweier Drehungen entspricht
gerade der Drehung um die Summe der beiden Winkel der einzelnen Drehungen. Eine
volle Umdrehung wird dabei wiederum mit keiner Drehung identifiziert.
Dreidimensionale Drehungen
Beschreibung durch Achse und Winkel
Eine Drehung im dreidimensionalen Raum lässt sich durch die Angabe einer
Drehachse, also eines Vektors
der Länge Eins auf der Einheitssphäre,
und eines Drehwinkels
beschreiben. Im Sonderfall
erhält man die identische Abbildung; für andere Winkel, auch im Fall einer
Geradenspiegelung mit
,
ist die Achse eindeutig festgelegt. Durch Wechsel der Orientierung der Drehachse
lässt sich eine Drehung um
auch als eine Drehung mit Winkel
auffassen.
Die zugehörige Drehung
lässt sich durch eine zugehörige Drehmatrix
explizit angegeben (siehe dort).
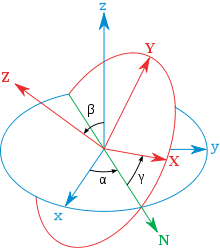
Beschreibung durch Eulersche Winkel
Auf Leonhard
Euler geht eine andere Beschreibung von Drehungen über drei Winkel, die
sogenannten eulerschen
Winkel, zurück. Ausgehend von der Standardbasis
zeigte Euler, dass sich jede Drehung
als
schreiben lässt.
Dabei sind die drei Winkel mit der Einschränkung
bis auf singuläre Bereiche eindeutig bestimmt: Etwa für
reicht einer der beiden anderen Winkel aus.
Die eulerschen Winkel werden häufig in der Physik verwendet; beispielsweise beruht die Beschreibung der Bahnen von Planeten oder Asteroiden durch die sogenannten Bahnelemente darauf.
Beschreibung mittels Quaternionen
Die Hamiltonschen Quaternionen
gestatten eine sehr elegante Beschreibung räumlicher Drehungen. Die Quaternionen
bilden eine vierdimensionale Algebra
über den reellen Zahlen. Als Basis verwendet man vier besondere Quaternionen,
nämlich
und
.
Hierbei ist
(die Multiplikation ist also nicht kommutativ) und es gelten die folgenden von
William
Rowan Hamilton angegebenen Rechenregeln:
.
Mit dieser Multiplikationsvorschrift – verschiedene, mathematisch exakte
Konstruktionen der Quaternionenalgebra finden sich hier
– wird
sogar zu einem Schiefkörper:
Zu jeder von null verschiedenen Quaternion
lässt sich eine inverse Quaternion
berechnen, für die
gilt.[1]
Eine Quaternion heißt rein, wenn sie sich als Linearkombination der
drei Basisvektoren
und
schreiben lässt. Vermöge der linearen Einbettung
mit ,
und
identifizieren wir den
mit den reinen Quaternionen. Nun lässt sich die Multiplikationsregel für
Quaternionen geometrisch deuten: Das Produkt zweier reiner Quaternionen
und
ist zwar nicht wieder rein, aber es gilt
Der reine Anteil des Produktes zweier reiner Quaternionen entspricht also
ihrem Kreuzprodukt, während der
skalare Anteil (der Koeffizient vor dem Basisvektor )
das Negative ihres Skalarprodukts
darstellt.
Um nun die Drehung
durch eine Quaternion zu beschreiben, benötigen wir zunächst einen Winkel
,
dessen Doppeltes,
dem gegebenen
entspricht. Neben
leistet dies auch
.
Wir betrachten nun die Quaternion
Diese Quaternion hat Länge Eins (bezüglich des Standardskalarprodukts in
)
und ihr Inverses lautet
Nimmt man nun eine beliebige reine Quaternion ,
so lässt sich leicht nachweisen, dass die mit
konjugierte
Quaternion
wieder eine reine Quaternion ist (wodurch sie sich erst als
für genau ein
darstellen lässt). Dabei gilt nun
Mit anderen Worten: die Konjugation mit
wirkt auf den reinen Quaternionen wie die Drehung
.
Universelle Überlagerung der SO(3)
Die oben beobachtete Zweideutigkeit bei der Wahl von
geht einher mit den beiden möglichen Vektoren zur Beschreibung der Achse: Eine
bestimmte Drehung lässt sich genau durch zwei zueinander inverse
Einheitsquaternionen beschreiben. Rein topologisch handelt es sich bei der Menge
der Einheitsquaternionen
offenbar um die dreidimensionale Einheitssphäre
im vierdimensionalen Raum. Die Quaternionenmultiplikation verleiht ihr eine
Lie-Gruppenstruktur. Als solche ist sie isomorph zur speziellen
unitären Gruppe
.
Wie im vorangegangenen Abschnitt diskutiert, liefert die Konjugation mit einer
Einheitsquaternion
eine Drehung. Offenbar handelt es sich hierbei um einen surjektiven
Gruppenhomomorphismus, der in einer genügend kleinen Umgebung von
einen Diffeomorphismus auf sein Bild in
darstellt. Mit anderen Worten, die Abbildung
ist eine zweiblättrige Überlagerung.
Da
einfach
zusammenhängend ist, handelt es sich um die universelle Überlagerung der
.
Um die anschauliche Bedeutung dieser universellen Überlagerung zu verstehen,
betrachten wir den Satz
vom Fußball. Durch geeignete Markierungen auf dem Ball lässt sich
prinzipiell zu jedem Zeitpunkt die Drehung bestimmen, die der Ball seit dem
Anstoß vollzogen hat. Dies ergibt einen stetigen Weg durch die ,
der bei der Einheitsmatrix beginnt. Beschreibt man die Einheitsmatrix etwa durch
das Einselement von
(alternativ könnte man das antipodal
gegenüberliegende Element in
also
verwenden), so lässt sich nun der gesamte Weg in stetiger Weise zu einem Weg
durch die
liften. Selbst wenn man den Ball zu Beginn der zweiten Halbzeit den Markierungen
entsprechend exakt gleich orientiert wieder auf dem Anstoßpunkt positioniert
(damit endet der Weg durch die
wieder im Punkt der Einheitsmatrix), so ist nicht garantiert, dass auch der
geliftete Weg wieder bei der Eins-Quaternion
angelangt ist. Mit einer Wahrscheinlichkeit von 50 % endet Letzterer
vielmehr in der
;
dann müsste man den Ball noch einmal um 360° bezüglich einer beliebig gewählten
Achse drehen, um auch den gelifteten Weg in seinem Ausgangspunkt enden zu
lassen. Da es keine höherblättrige Überlagerung der
gibt, ist es nicht möglich, die allgemeine Drehungen im Raum in konsistenter
Weise noch feinstufiger zu erfassen.
Bemerkenswerterweise verwendet man in der Quantenmechanik
die
und nicht die
als Zustandsraum zur Beschreibung des Spins
eines Teilchens.
Topologie der SO(3)
Jede Faser der soeben beschrieben Überlagerung
besteht aus zwei Antipodenpunkten (entsprechend den beiden Möglichkeiten für
die Wahl von
mit
)
der
.
Folglich ist die
homöomorph
zum Quotienten von
bei Identifizierung
gegenüberliegender Punkte. Dies ergibt aber genau den dreidimensionalen reell-projektiven Raum
.
Endliche Untergruppen der SO(3)
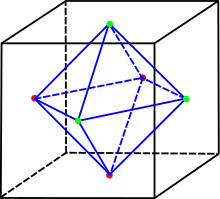
Die endlichen Untergruppen der
stehen in einem engen Zusammenhang mit Raumkörpern, die eine endliche Zahl von
Symmetrien aufweisen. Da bei einer beliebigen Drehung etwa eines Würfels im Raum
die zugehörige Untergruppe mit ebendieser Drehung konjugiert wird, interessiert
man sich nur für die Konjugationsklassen der endlichen Untergruppen der
.
Diese sind:
- Die zyklische
Gruppen
für
, erzeugt von einer Drehung um den
-ten Teil eines Vollwinkels
; für
sind sie Teil der vollen Drehgruppe eines geraden Prismas über einem regulären
-Eck.
- Die volle Drehgruppe eines solchen Prismas. Sie enthält neben der bereits
beschriebenen
auch diejenigen Drehungen, die auf dem regelmäßigen
-Eck wie Achsenspiegelungen wirken, aber durch gleichzeitiges Spiegeln an der Trägerebene des
-Ecks zu Drehungen des Raums werden. Es handelt sich um die Diedergruppen
der Ordnung
(formal für
; geometrische Deutung für
).
- Die volle Drehgruppe
eines regulären Tetraeders. Sie ist isomorph zur alternierenden Gruppe
der Ordnung
.
- Die volle Drehgruppe
eines regulären Oktaeders, die sogenannte Oktaedergruppe der Ordnung
. Sie ist gleichzeitig für den zum Oktaeder dualen Würfel zuständig. Sie ist isomorph zur symmetrischen Gruppe
.
- Die volle Drehgruppe
eines regulären Ikosaeders (siehe Ikosaedergruppe) der Ordnung
. Sie beschreibt zugleich die Drehungen des Dodekaeders und ist isomorph zur alternierenden Gruppe
.
Drehgruppen von Figuren
Das Wort Drehgruppe wird auch als Bezeichnung für jene Untergruppe der Symmetrien eines
bestimmten geometrischen Objektes
gebraucht, die eine planimetrische
Figur oder einen stereometrischen
Körper durch Drehung auf sich selbst abbildet. Eine solche Drehgruppe ist dann
eine (meist endliche) Untergruppe der
oder der
und besteht genau aus allen jenen Drehungen, durch die diese Figur bzw. dieser
Körper in sich selbst überführt wird.
Beispiele
- in der Ebene
-
- Die Drehgruppe einer Strecke
stimmt mit ihrer Symmetriegruppe überein und besteht nur aus zwei Elementen:
der Identität
und der Drehung um 180° um den Mittelpunkt. Sie ist also isomorph zur symmetrischen
Gruppe
.
- Die Drehgruppe eines regulären
Vielecks mit
. Diese ist ein Normalteiler der zugehörigen Symmetriegruppe, der Diedergruppe
.
- Die Drehgruppe einer Strecke
stimmt mit ihrer Symmetriegruppe überein und besteht nur aus zwei Elementen:
der Identität
und der Drehung um 180° um den Mittelpunkt. Sie ist also isomorph zur symmetrischen
Gruppe
- im dreidimensionalen Raum
-
- Die Drehgruppe des Tetraeders,
eine Untergruppe der Tetraedergruppe,
enthält 12 Elemente (Drehungen um 3- und 2-zählige Achsen) und ist isomorph
zur alternierenden Gruppe
auf der Menge der vier Ecken. Ihr Schoenflies-Symbol ist
.
- Die Drehgruppe des Oktaeders
und die des zu ihm dualen
Würfels,
eine Untergruppe der Oktaedergruppe,
enthält 24 Elemente (Drehungen um 4-, 3- und 2-zählige Achsen) und ist
isomorph zur symmetrischen Gruppe
auf der Menge der vier 3-zähligen Achsen. Ihr Schoenflies-Symbol ist
.
- Die Drehgruppe des Ikosaeders
und die des zu ihm dualen Dodekaeders,
eine Untergruppe der Ikosaedergruppe,
enthält 60 Elemente (Drehungen um 5-, 3- und 2-zählige Achsen) und ist
isomorph zur alternierenden Gruppe
. Ihr Schoenflies-Symbol ist
.
- Die Drehgruppe des Tetraeders,
eine Untergruppe der Tetraedergruppe,
enthält 12 Elemente (Drehungen um 3- und 2-zählige Achsen) und ist isomorph
zur alternierenden Gruppe
Anwendungen
- Satz
vom Fußball – Anschauliche Anwendung der Drehgruppe
.
Literatur
- Horst Knörrer: Geometrie (= Vieweg-Studium. Band 71). Vieweg, Braunschweig u.a. 1996, ISBN 3-528-07271-7.
- Uwe Storch, Hartmut Wiebe: Lehrbuch der Mathematik. Band 2: Lineare Algebra. BI-Wissenschafts-Verlag, Mannheim 1990, ISBN 3-411-14101-8.
Anmerkungen
- ↑
Es ist nämlich
ein reelles Vielfaches der
.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 05.08. 2021