Galoisgruppe

Die Galoisgruppe (nach Évariste Galois) ist eine Gruppe, mit deren Hilfe Körpererweiterungen in der Algebra untersucht werden können.

Die Zwischenkörper einer Körpererweiterung lassen sich gewissen Untergruppen der Galoisgruppe zuordnen. Damit kann man Strukturuntersuchungen von Körpererweiterungen mit gruppentheoretischen Untersuchungen in Verbindung bringen. Da zu endlichdimensionalen Körpererweiterungen endliche Galoisgruppen gehören, können damit solche Strukturuntersuchungen oft stark vereinfacht werden.

Historisch bedeutsam war, dass die klassischen Fragen der Konstruierbarkeit – mit Zirkel und Lineal – gewisser algebraischer Zahlen damit in eine gruppentheoretische Formulierung übersetzt werden konnten. Einzelheiten zur klassischen Fragestellung der Konstruierbarkeit mit Zirkel und Lineal, Beispiele und deren moderne Lösung siehe unter → Konstruierbares Polygon.

Definition

Sei F/K (lies: „ über “) eine Körpererweiterung. Das heißt: und sind Körper und der Körper ist als Unterring in enthalten. Damit ist zugleich ein (nicht notwendig endlichdimensionaler) -Vektorraum.

In dieser Situation heißt die Gruppe aller Körperautomorphismen des Erweiterungskörpers , die den Grundkörper elementweise festlassen, die Galoisgruppe von über und wird mit $\mathrm {Gal} (F/K)$ bezeichnet, formal

$\mathrm {Gal} (F/K)=\lbrace \varphi \in \mathrm {Aut} (F)\mid \forall k\in K:\varphi (k)=k\rbrace$ .

Dies kann auch so formuliert werden: Die Galoisgruppe von über besteht genau aus den Körperautomorphismen von , die zugleich Vektorraumendomorphismen von als -Vektorraum sind.

Galoisgruppe eines Polynoms

Sei ein Körper. Als Galoisgruppe des Polynoms im Polynomring K[x] wird die Gruppe $\mathrm {Gal} (F/K)$ bezeichnet, wobei ein Zerfällungskörper des Polynoms ist. Man spricht in diesem Fall auch von dem Zerfällungskörper, da Zerfällungskörper – und damit die Galoisgruppe eines Polynoms – bis auf Isomorphie eindeutig bestimmt sind.

Der Zerfällungskörper eines Polynoms ist normal über dem Grundkörper . In diesem Fall ist die – hier endlichdimensionale – Körpererweiterung F/K bereits dann galoissch, wenn die über irreduziblen Faktoren von separabel sind. Der Artikel Galoistheorie behandelt den Begriff der Galoisgruppe eines Polynoms, für diesen Fall genügt die unten genannte erste Fassung des Hauptsatzes – der Hauptsatz für endliche Galoiserweiterungen.

Abweichende Bedeutungen des Begriffs

Besonders nützlich ist die Galoisgruppe, wenn die Körpererweiterung F/K eine Galoiserweiterung (s. u.) ist. In der Literatur wird oft nur in diesem Falle von „Galoisgruppe“ gesprochen. Die in diesem Artikel verwendete Gruppe der -Automorphismen von wird dann mit $\mathrm {Aut} _{K}(F)$ bezeichnet.

Eigenschaften

Die Galoisgruppe ist eine Untergruppe der Automorphismengruppe von .
Ist die Körpererweiterung endlich, d.h. ist endlichdimensional über , so ist die Gruppenordnung von $\mathrm {Gal} (F/K)$ kleiner gleich dem Erweiterungsgrad . In diesem Fall existiert für jedes Körperelement $\alpha \in F$ das Minimalpolynom $f=m_{K,\alpha }$ von $\alpha$ über . Ist eine endliche Galoiserweiterung, dann gilt $|\mathrm {Gal} (F/K)|=[F:K]$ .
Sei ein Zerfällungskörper des Polynoms über . Jeder Automorphismus aus der Galoisgruppe $\mathrm {Gal} (F/K)$ des Polynoms bildet eine Nullstelle von wieder auf eine Nullstelle ab. Die Galoisgruppe operiert also auf der Menge der Nullstellen von im Körper , $N=\{u_{1},u_{2},\ldots u_{n}\}$ als Permutationsgruppe und ist damit isomorph zu einer Untergruppe der symmetrischen Gruppe $S_{n}$ . Für ein separables, über irreduzibles Polynom ist diese Operation sogar transitiv, das heißt zu zwei verschiedenen Nullstellen $u_{j}\neq u_{k}$ gibt es ein Element $\varphi$ der Galoisgruppe, das $u_{j}$ auf $u_{k}$ abbildet: $\varphi (u_{j})=u_{k}$ .

Galoiskorrespondenz, Abgeschlossene Untergruppen und Zwischenkörper

Man kann jedem Zwischenkörper der Erweiterung F/K die Untergruppe der Galoisgruppe $G=\mathrm {Gal} (F/K)$ zuordnen, deren Elemente elementweise fest lässt, und umgekehrt jeder Untergruppe von $\mathrm {Gal} (F/K)$ den Zwischenkörper, den sie fixiert. Nach Hungerford (1981) wird hier für beide Zuordnungen, die beide auch als Galoiskorrespondenz bezeichnet werden, die „Priming-Notation“ verwendet:

$H^{\prime }:=\{f\in F\,|\,\forall \eta \in H:\eta (f)=f\}$

Für Zwischenkörper und der Erweiterung, Untergruppen und von gelten folgende Beziehungen:

$F^{\prime }=1$ und $K^{\prime }=G$ ,
$1^{\prime }=F$ ,
$L\subset M\Rightarrow M^{\prime }<L^{\prime }$ ,
$H<J\Rightarrow J^{\prime }\subset H^{\prime }$ ,
$L\subset L^{\prime \prime }$ und $H<H^{\prime \prime }$ ,
$L^{\prime }=L^{\prime \prime \prime }$ und $H^{\prime }=H^{\prime \prime \prime }$ .

Die Körpererweiterung F/K heißt hier Galoiserweiterung, wenn sie normal und separabel ist. Dies ist genau dann der Fall, wenn $G^{\prime }=K$ gilt, wenn also die Galoisgruppe außer dem Grundkörper keine weiteren Elemente von fixiert. Da in allen Fällen $K^{\prime }=G$ gilt, ist die Erweiterung genau dann galoissch, wenn $K=K^{\prime \prime }$ ist. Dieselbe Bedingung gilt für Zwischenkörper : Die Erweiterung F/L ist genau dann eine Galoiserweiterung, wenn $L=L^{\prime \prime }$ gilt. Die Begriffe normal und separabel werden im Artikel Körpererweiterung unabhängig von den hier verwendeten Zuordnungen definiert. Dort wird im Abschnitt Galoiserweiterung dieselbe für den Fall definiert, dass die Erweiterung algebraisch ist. Die hier verwendete Definition lässt nach Emil Artin und Hungerford (1981) auch nicht algebraische Erweiterungen zu.

Abgeschlossenheit

Nach Hungerford (1981) heißt eine Untergruppe der Galoisgruppe oder ein Zwischenkörper der Erweiterung abgeschlossen, wenn $X=X^{\prime \prime }$ gilt.

Alle Objekte $X=Y^{\prime }$ , die als Bilder der oben beschriebenen Korrespondenzen auftreten, sind abgeschlossen (nach 6.).
Die triviale Untergruppe 1, und sind abgeschlossen.
Die Erweiterung ist genau dann eine Galoiserweiterung, wenn abgeschlossen ist.

Mit den am Anfang des Abschnitts vereinbarten Bezeichnungen gilt:

Wenn abgeschlossen ist und endlich ist, dann ist abgeschlossen und es gilt $[L^{\prime }:M^{\prime }]=[M:L]$ .
Wenn abgeschlossen ist und endlich ist, dann ist abgeschlossen und $[H^{\prime }:J^{\prime }]=[J:H]$ .
Speziell gilt (für ): Jede endliche Untergruppe der Galoisgruppe ist abgeschlossen.
Wenn eine endlichdimensionale Galoiserweiterung von ist, dann sind alle Zwischenkörper und alle Untergruppen der Galoisgruppe abgeschlossen und die Galoisgruppe hat die Ordnung .

Hauptsätze der Galoistheorie

Endlichdimensionale Körpererweitung

Ist eine endlichdimensionale Galoiserweiterung von , dann vermittelt die Galoiskorrespondenz eine Bijektion zwischen der Menge der Zwischenkörper und der Menge der Untergruppen der Galoisgruppe. Diese Korrespondenz bildet den Teilmengenverband der Zwischenkörper (mit der Ordnung $\subset$ ) auf den Verband der Untergruppen (mit der Ordnung ) ordnungstreu ab, wobei die Teilmengenbeziehung umgekehrt wird. Dabei gilt:

Die relative Dimension von zwei Zwischenkörpern ist gleich dem relativen Index der korrespondierenden Untergruppen.
ist galoissch über jedem Zwischenkörper . Die Galoisgruppe $\mathrm {Gal} (F/L)$ stimmt mit der Untergruppe $L^{\prime }$ überein.
Ein Zwischenkörper ist galoissch über genau dann, wenn die korrespondierende Untergruppe $L^{\prime }$ ein Normalteiler der Galoisgruppe $G=\mathrm {Gal} (F/K)$ ist. In diesem Fall ist die Faktorgruppe $G/L^{\prime }$ isomorph zur Galoisgruppe $\mathrm {Gal} (L/K)$ des Körpers über .

Unendlichdimensionale algebraische Erweiterung

Ist eine algebraische, nicht notwendig endlichdimensionale Galoiserweiterung von , dann vermittelt die Galoiskorrespondenz eine Bijektion zwischen der Menge aller Zwischenkörper und der Menge der abgeschlossenen Untergruppen der Galoisgruppe. Diese Korrespondenz bildet den Teilmengenverband der Zwischenkörper (mit der Ordnung $\subset$ ) auf den Verband der abgeschlossenen Untergruppen (mit der Ordnung ) ordnungstreu ab, wobei die Teilmengenbeziehung umgekehrt wird. Dabei gilt:

ist galoissch über jedem Zwischenkörper . Die Galoisgruppe $\mathrm {Gal} (F/L)$ stimmt mit der Untergruppe $L^{\prime }$ überein.
Ein Zwischenkörper ist galoissch über genau dann, wenn die korrespondierende Untergruppe $L^{\prime }$ ein Normalteiler der Galoisgruppe $G=\mathrm {Gal} (F/K)$ ist. In diesem Fall ist die Faktorgruppe $G/L^{\prime }$ isomorph zur Galoisgruppe $\mathrm {Gal} (L/K)$ des Körpers über .

Beispiele

Die komplexen Zahlen sind ein Körper und enthalten den Körper der reellen Zahlen. Also ist $\mathbb {C} /\mathbb {R}$ eine Körpererweiterung. Da $\mathbb {C}$ ein Vektorraum der Dimension 2 über $\mathbb {R}$ ist ( ist eine Basis), gilt $[\mathbb {C} :\mathbb {R} ]=2$ . Die Galoisgruppe enthält die Identität und die komplexe Konjugation. Die Wurzelmenge des Minimalpolynoms $f=X^{2}+1$ ist $\lbrace i,-i\rbrace$ . Die Identität bildet diese beiden Elemente wieder auf sich selbst ab, während sie von der komplexen Konjugation permutiert werden. Also ist die Galoisgruppe eingeschränkt auf die Wurzelmenge isomorph zur symmetrischen Gruppe $S_{2}$
Sei , der Körper der rationalen Funktionen $\rho$ über K. Dann ist für jede Zahl $a\in K\setminus \{0\}$ die durch $\varphi _{a}:\rho (x)\mapsto \rho (ax)$ definierte Abbildung ein K-Automorphismus. Ist der Körper K unendlich, so gibt es unendlich viele dieser Automorphismen und die Galoisgruppe $G=\mathrm {Gal} (F/K)$ ist eine unendliche Gruppe. Ist das Element $a\neq 0$ selbst keine Einheitswurzel, dann ist die von dem Automorphismus $\varphi _{a}$ erzeugte Untergruppe von G nicht abgeschlossen.
Der Körper der reellen Zahlen lässt keine nichttrivialen Automorphismen zu, denn seine Anordnung ist eine algebraische Invariante: Es ist $r\leq s$ für zwei reelle Zahlen genau dann, wenn ein Quadrat ist. Daher ist der Körper der reellen Zahlen über keinem seiner echten Teilkörper galoissch, dasselbe gilt für den Körper der reellen algebraischen Zahlen.
Allgemeiner trifft das auf alle euklidischen Körper zu: die Galoisgruppe eines euklidischen Körpers über einem seiner Teilkörper ist immer die triviale Gruppe.

Galoisgruppe eines kubischen Polynoms

Das folgende ausführliche Beispiel zeigt am Polynom $f(x)=x^{3}-2$ , wie mit Hilfe der Galoisgruppe Zwischenkörper bestimmt werden können.

Der von der reellen Zahl $\xi _{1}={\sqrt[{3}]{2}}$ über ${\mathbb {Q}}$ erzeugte Zahlkörper $L_{1}={\mathbb {Q}}\left({\sqrt[{3}]{2}}\right)$ hat die Galoisgruppe 1, da keine weiteren Nullstellen des Minimalpolynoms $f(x)=x^{3}-2$ von $\xi _{1}$ im (reellen!) Zahlkörper $L_{1}$ liegen. Diese Erweiterung ist also nicht galoissch. Ihr Grad ist 3, da $L_{1}$ isomorph zu dem Faktorring ${\mathbb {Q}}(x)/(f)$ ist (siehe Faktorring). Dasselbe gilt für die beiden Zahlkörper $L_{2}={\mathbb {Q}}(\xi _{2})$ und $L_{3}={\mathbb {Q}}(\xi _{3})$ , die von den beiden nichtreellen Wurzeln $\xi _{2}={\sqrt[{3}]{2}}\cdot \exp \left({\frac {2\pi i}{3}}\right)$ und $\xi _{3}={\sqrt[{3}]{2}}\cdot \exp \left({\frac {4\pi i}{3}}\right)$ von über ${\mathbb {Q}}$ erzeugt werden. Alle drei Körper sind isomorphe Zwischenkörper des Zerfällungskörpers des Polynoms .

Da der Grundkörper $\mathbb {Q}$ als Körper mit der Charakteristik 0 perfekt ist, ist der gesuchte Zerfällungskörper $F={\mathbb {Q}}(\xi _{1},\xi _{2},\xi _{3})$ eine Galoiserweiterung von ${\mathbb {Q}}$ und die Galoisgruppe muss transitiv auf den Nullstellen von operieren. Die einzige echte Untergruppe der symmetrischen Gruppe $S_{3}$ , die transitiv auf $\{1,2,3\}$ operiert, ist der von dem 3-Zyklus (1,2,3) erzeugte Normalteiler der $S_{3}$ , die alternierende Gruppe $A_{3}$ . Da wir bereits drei echte Zwischenkörper identifiziert haben und die $A_{3}$ keine echten Untergruppen hat, kann es sich noch nicht um die volle Galoisgruppe handeln. Diese kann also nur die volle symmetrische Gruppe sein, es gilt also

$\operatorname {Gal} (F/\mathbb {Q} )=S_{3}$ .

Neben den Zwischenkörpern, die wir schon identifiziert haben, muss noch ein normaler Zwischenkörper vorhanden sein, der zweidimensional über ${\mathbb {Q}}$ ist (Index von $A_{3}$ ). Dieser bleibt fix unter zyklischen Vertauschungen der Nullstellen, das trifft nur auf den Kreisteilungskörper der dritten Einheitswurzeln zu, der durch die Einheitswurzel $\omega =\exp \left({\frac {2\pi i}{3}}\right)={\frac {\xi _{2}}{\xi _{1}}}={\frac {\xi _{3}}{\xi _{2}}}={\frac {\xi _{1}}{\xi _{3}}}$ erzeugt wird. Alle Ergebnisse werden in dem Diagramm unten gezeigt.

Untergruppenverband der Galoisgruppe und Zwischenkörperverband der Körpererweiterung F im Beispiel. Die Pfeile im linken Diagramm sind als „ist Untergruppe von“ (dünn) bzw. „ist Normalteiler von“ (dick) zu lesen, im rechten Diagramm als „ist Erweiterung von“ (dünn) bzw. „ist Galoiserweiterung von“ (dick). Die Zahlen an den Pfeilen bedeuten im linken Diagramm relative Indizes, im rechten Diagramm die relative Dimension der Erweiterung. Schiebt man die beiden Graphen übereinander, so kommen die Objekte aufeinander zu liegen, die einander bei der Galoiskorrespondenz entsprechen. So wird z.B. der reelle Körper L1 durch die Gruppe <(2,3)> fixiert, der erzeugende Automorphismus, der die beiden nichtreellen Wurzeln von f vertauscht, ist auf F die Einschränkung der komplexen Konjugation.

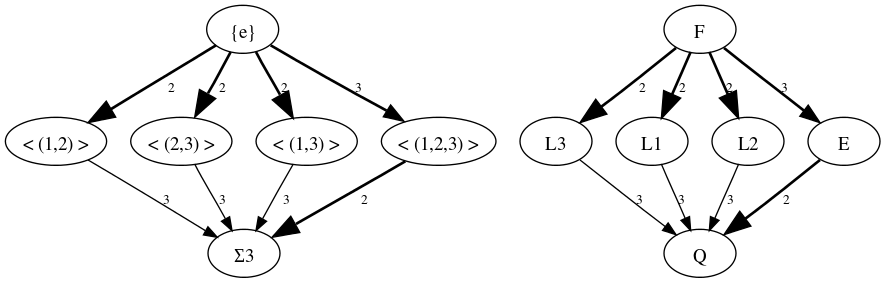
Die Zwischenkörper können nun unter anderem dazu verwendet werden, verschiedene Darstellungen des Zerfällungskörpers zu gewinnen:

$F={\mathbb {Q}}(\xi _{1},\xi _{2},\xi _{3})$ , dies folgt – ganz ohne Galoistheorie – aus seiner Definition als Zerfällungskörper.
$F={\mathbb {Q}}(\xi _{1},\xi _{2})$ : Dass zwei Nullstellen zur Erzeugung genügen, folgt aus der Tatsache, dass zwischen den Körpern, die durch eine Nullstelle erzeugt werden und keine weiteren Körper liegen.
$F=E(\xi _{1})={\mathbb {Q}}(\omega ,\xi _{1})$ : Hier wird die (in diesem Fall einzige maximale) Subnormalreihe der Galoisgruppe nachgebildet (in der Graphik der Pfad rechts außen). Die relativen Erweiterungen in /SPAN> ${\mathbb {Q}}\subset E\subset E(\xi _{1})$ sind alle galoissch und ihre Galoisgruppen sind einfache abelsche Gruppen.
lässt sich auch als einfache Körpererweiterung darstellen: $\omega +\xi _{1}$ ist sicher ein Element von und wird von keinem nichttrivialen Element der Galoisgruppe fixiert. Daher ist $F={\mathbb {Q}}(\omega +\xi _{1})$ .

Natürlich können in allen genannten Darstellungen die Nullstellen $\xi _{k}$ beliebig ausgetauscht werden.

Basierend auf einem Artikel in:

Wikipedia.de