Kolimes

Der Kolimes oder Colimes ist eine mathematische Konstruktion, mit der man aus gegebenen Objekten und Morphismen zwischen ihnen neue Objekte und Morphismen erhält. Ein wichtiger Spezialfall ist der sogenannte filtrierte oder induktive Limes, den man sich grob als eine aufsteigende Vereinigung von Objekten vorstellen kann. Die abstrakte Definition in der Kategorientheorie umfasst diesen Spezialfall, sie ist, wie der Name schon andeutet, dual zur Bildung des Limes.

Erste Definition

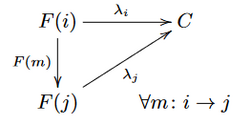
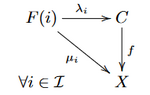
Sei ${\mathcal {C}}$ eine Kategorie. Weiter sei ein Funktor $F\colon {\mathcal {I}}\rightarrow {\mathcal {C}}$ gegeben. Ein Kolimes von $F$ ist ein Objekt $C$ aus ${\mathcal {C}}$ zusammen mit einer Familie $(\lambda _{i})_{i\in {\mathcal {I}}}$ von Morphismen $\lambda _{i}\colon F(i)\rightarrow C$ , so dass folgendes gilt:

Für jeden Morphismus $m\colon i\rightarrow j$ in ${\mathcal {I}}$ gilt $\lambda _{j}\circ F(m)=\lambda _{i}$ .
Das Paar $(C,(\lambda _{i})_{i\in {\mathcal {I}}})$ ist universell mit dieser Eigenschaft, das heißt:

Ist $(X,(\mu _{i})_{i\in {\mathcal {I}}})$ ein weiteres Paar, bestehend aus einem Objekt $X$ aus ${\mathcal {C}}$ und Morphismen $\mu _{i}\colon F(i)\rightarrow X$ mit $\mu _{j}\circ F(m)=\mu _{i}$ für alle Morphismen $m\colon i\rightarrow j$ in ${\mathcal {I}}$ , so gibt es genau einen Morphismus $f\colon C\rightarrow X$ mit $f\circ \lambda _{i}=\mu _{i}$ für alle Objekte $i\in {\mathcal {I}}$ .^[1]^[2]

Ein solches Paar $(C,(\lambda _{i})_{i\in {\mathcal {I}}})$ ist, wie bei universellen Eigenschaften üblich, bis auf (eindeutige) Isomorphie eindeutig bestimmt. Man spricht daher von dem Kolimes. Gängige Bezeichnungen sind

$\operatorname {colim} F,\quad \operatorname {colim} _{i\in {\mathcal {I}}}F(i),\quad \lim _{{\mathcal {I}}\rightarrow }F$ oder $\lim _{\rightarrow {\mathcal {I}}}F$ .

(Beachte, dass der Limes mit dem umgekehrten Pfeil $\lim _{\leftarrow {\mathcal {I}}}$ bezeichnet wird.)

Beispiel induktiver Limes

Zum besseren Verständnis obiger Definition stellen wir die Verbindung zum induktiven Limes bezüglich einer partiell geordneten Menge $(I,\leq )$ her. In diesem Fall ist ${\mathcal {I}}$ die Kategorie mit

Objekten: Elemente $i\in I$
Morphismen: Zwischen je zwei Objekten $i,j\in I$ mit $i\leq j$ gibt es genau einen Morphismus $m_{i,j}\colon i\rightarrow j$ .

Ein Funktor $F\colon {\mathcal {I}}\rightarrow {\mathcal {C}}$ ordnet jedem Index $i\in I$ ein Objekt $X_{i}=F(i)$ zu und für $i\leq j$ hat man Morphismen $f_{i,j}=F(m_{i,j})\colon X_{i}\rightarrow X_{j}$ . Die Funktoreigenschaften besagen gerade, dass $f_{i,i}=\mathrm {id} _{X_{i}}$ und $f_{i,k}=f_{j,k}\circ f_{i,j}$ für alle $i\leq j\leq k$ . Dies zeigt, dass obige Definition des Kolimes die Definition des induktiven Limes verallgemeinert. Derartige Kolimites heißen auch direkte Limites. Die scheinbare Inkonsistenz in diesen Bezeichnungen, dass direkte oder induktive Limites kategorientheoretisch Kolimites sind, hat historische Gründe.^[3]

Beispiel leerer Kolimes

Ein leerer Kolimes ist ein Anfangsobjekt.

Ist ${\mathcal {I}}=\emptyset$ in obiger Definition gleich der leeren Kategorie, so ist jeder Funktor $F\colon {\mathcal {I}}\rightarrow {\mathcal {C}}$ ebenfalls leer. Ein Objekt $C$ (zusammen mit einer leeren Familie von Morphismen $(\lambda _{i})_{i\in \emptyset }$ ) ist nach obiger Definition genau dann Kolimes, wenn es zu jedem Objekt $X$ (zusammen mit einer leeren Familie von Morphismen) genau einen Morphismus $f\colon C\rightarrow X$ gibt (so dass eine leere Menge von Bedingungen erfüllt ist), und das bedeutet gerade, dass $C$ ein Anfangsobjekt (initiales Objekt) ist.

Dieses Beispiel zeigt auch, dass ein beliebiger Kolimes nicht immer existieren muss, denn es gibt ja Kategorien ohne initiale Objekte. Wir werden in der zweiten Definition sehen, dass jeder Kolimes ein Anfangsobjekt einer geeigneten Kategorie ist.

Spezielle Kolimites

Weitere Konstruktionen erweisen sich, je nach Wahl der Indexkategorie, ${\mathcal {I}}$ als Spezialfälle eines Kolimes:^[4]

$I$	universelle Konstruktion
Beliebig viele Objekte, nur Identitäten	Koprodukt
$\varnothing$	Anfangsobjekt
	Differenzkokern
	Kofaserprodukt

Zweite Definition

Sei ${\mathcal {C}}$ eine Kategorie $F\colon {\mathcal {I}}\rightarrow {\mathcal {C}}$ ein Funktor. Für jedes Objekt $X$ in ${\mathcal {C}}$ sei der konstante Funktor ${\mathcal {I}}\rightarrow {\mathcal {C}}$ , der jedes Objekt auf $X$ und jeden Morphismus auf den identischen Morphismus $1_{X}$ abbildet, mit $K_{X}$ bezeichnet.

Sei ${\mathcal {C}}_{F}$ die sogenannte Kategorie der Kegel unter $F$ , das heißt die Kategorie mit

Objekten: Kegel unter $F$ , das heißt natürlichen Transformationen $\lambda =(\lambda _{i})_{i\in {\mathcal {I}}}\colon F\Rightarrow K_{X}$ für Objekte $X$ aus ${\mathcal {C}}$ .
Morphismen von $\lambda \colon F\Rightarrow K_{X}$ nach $\mu \colon F\Rightarrow K_{Y}$ : ${\mathcal {C}}$ -Morphismen $f\colon X\rightarrow Y$ , so dass $f\circ \lambda _{i}=\mu _{i}$ .

Ein Kolimes ist ein Anfangsobjekt in ${\mathcal {C}}_{F}$ .^[5]

Das ist nur ein Umformulierung der ersten Definition. Die Morphismenfamilien der ersten Definition werden hier als natürliche Transformationen gedeutet.

Dritte Definition

Sei ${\mathcal {C}}$ eine Kategorie $F\colon {\mathcal {I}}\rightarrow {\mathcal {C}}$ ein Funktor.

Dann gibt es einen Funktor $\mathrm {Cone} (F,K_{-}):{\mathcal {C}}\rightarrow {\mathcal {Set}}$ in die Kategorie der Mengen, der Objekte aus ${\mathcal {C}}$ auf die Menge der Kegel $\lambda \colon F\Rightarrow K_{X}$ mit Ziel $K_{X}$ abbildet und einen Morphismus $f\colon X\rightarrow Y$ auf die Abbildung, die einem Kegel $\lambda =(\lambda _{i})_{i\in {\mathcal {I}}}\colon F\Rightarrow K_{X}$ den Kegel $(f\circ \lambda _{i})_{i\in {\mathcal {I}}}\colon F\Rightarrow K_{Y}$ zuordnet.

Ein Kolimes von $F$ ist eine Darstellung des Funktors $\mathrm {Cone} (F,K_{-})$ .^[6]

Bemerkungen

In dieser dritten Definition muss die Kategorie ${\mathcal {I}}$ klein sein, damit die Kegel Mengen sind und daher die Menge der Kegel überhaupt betrachtet werden kann. In den vorangegangenen Definitionen musste ${\mathcal {I}}$ nicht notwendig klein sein, allerdings wendet man derartige Konstruktionen in der Regel auf kleine Indexkategorien ${\mathcal {I}}$ an, wie alle genannten Beispiele belegen.

Die Darstellbarkeit bedeutet, dass es ein Objekt $C$ in ${\mathcal {C}}$ gibt und einen natürlichen Isomorphismus $\alpha =(\alpha _{X})_{X\in {\mathcal {C}}}:\mathrm {Cone} (F,K_{-})\rightarrow \mathrm {Hom} _{\mathcal {C}}(C,-)$ . Für jedes Objekt $X$ hat man also eine bijektive Abbildung $\alpha _{X}\colon \mathrm {Cone} (F,K_{X})\rightarrow \mathrm {Hom} _{\mathcal {C}}(C,X)$ und die Natürlichkeit sichert, dass es zu jedem Kegelmorphismus genau einen Morphismus $C\rightarrow X$ gibt, so dass eine Verträglichkeitsbedingung wie in der ersten Definition erfüllt ist.

Einzelnachweise

↑ Horst Herrlich, George E. Strecker: Category Theory. Allyn and Bacon Inc., 1973, ISBN 0-205-56332-5, Definition 20.2, S. 134.
↑ Saunders Mac Lane: Categories for the Working Mathematician. 2. Auflage. Springer, 1998, ISBN 0-387-98403-8, Kapitel III.3 Coproducts and Colimits.
↑ Horst Herrlich, George E. Strecker: Category Theory. Allyn and Bacon Inc., 1973, ISBN 0-205-56332-5, §22 Inverse and direct limits.
↑ Emily Riehl: Category Theory in Context. AMS Dover Publications, 2016, ISBN 978-0-486-80903-8, Definition 3.1.23, S. 80.
↑ Emily Riehl: Category Theory in Context. AMS Dover Publications, 2016, ISBN 978-0-486-80903-8, Definition 3.1.6, S. 75.
↑ Emily Riehl: Category Theory in Context. AMS Dover Publications, 2016, ISBN 978-0-486-80903-8, Definition 3.1.5, S. 75.

Basierend auf einem Artikel in:

Wikipedia.de