Schlangenlemma

Das Schlangenlemma, eine in allen abelschen Kategorien gültige Aussage aus dem mathematischen Teilgebiet der homologischen Algebra, ist ein Werkzeug zur Konstruktion der dort betrachteten langen exakten Sequenzen. Wichtige Anwendungen findet es beispielsweise in der algebraischen Topologie. Die mit dem Schlangenlemma konstruierten Homomorphismen werden üblicherweise als Verbindungshomomorphismen bezeichnet.

Aussage

In einer abelschen Kategorie (etwa der Kategorie der abelschen Gruppen oder der Vektorräume über einem gegebenen Körper) sei das folgende kommutative Diagramm gegeben:

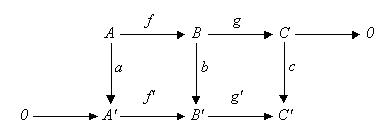
Hierbei seien die Zeilen exakt und $0$ bezeichne das Nullobjekt. Dann gibt es eine exakte Sequenz, die die Kerne und Kokerne von , , in Beziehung setzt:

$\ker a\;{\color {Gray}\longrightarrow }\ker b\;{\color {Gray}\longrightarrow }\ker c\;{\overset {d}{\longrightarrow }}\operatorname {coker}a\;{\color {Gray}\longrightarrow }\operatorname {coker}b\;{\color {Gray}\longrightarrow }\operatorname {coker}c$

Ist außerdem ein Monomorphismus, so ist das auch der Morphismus $\ker a\to \ker b$ . Ist ein Epimorphismus, so gilt das auch für $\operatorname {coker}b\to \operatorname {coker}c$ .

In der Kategorie der Gruppen gilt das Schlangenlemma dagegen nur unter Zusatzvoraussetzungen an die Homomorphismen , , (siehe unten).

Herkunft des Namens

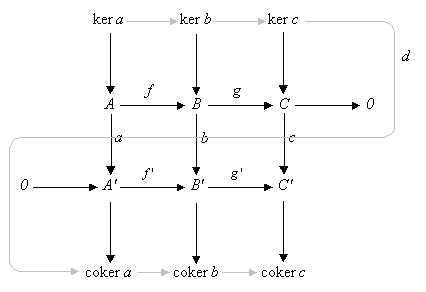
Erweitert man das Diagramm um Kerne und Kokerne, so sieht man, wie sich die behauptete exakte Sequenz durch das Diagramm „schlängelt“:

Beweis

Für den Beweis nimmt man zunächst an, dass das Diagramm die Kategorie der Moduln über einem Ring betrifft. Dies gestattet es, die Behauptung durch Diagrammjagd nachzuweisen. Die Gültigkeit für den Fall einer beliebigen abelschen Kategorie ergibt sich dann aus dem Einbettungssatz von Mitchell.

Konstruktion der Homomorphismen

Die Homomorphismen zwischen den Kernen bzw. Kokernen werden in natürlicher Weise von den gegebenen horizontalen Homomorphismen über die universellen Eigenschaften von Kern bzw. Kokern induziert. Die wesentliche Aussage des Lemmas ist die Existenz des Verbindungshomomorphismus , der die Sequenz vervollständigt.

Im Falle der Kategorie abelscher Gruppen oder von Moduln über einem Ring kann man elementweise durch Diagrammjagd konstruieren: Sei $x\in \operatorname {ker}\,c$ gegeben, d.h. ein $x\in C$ mit c(x)=0 . Wegen der Surjektivität von gibt es ein $y\in B$ mit g(y)=x . Wegen g'(b(y))=c(g(y))=0 gibt es ein (wegen der Injektivität von eindeutiges) $z\in A'$ mit f'(z)=b(y) . Definiere d(x) als das Bild von in $\operatorname {coker}\,a$ .

Die Wahl von $y\in B$ war hierbei nicht eindeutig, wegen der Exaktheit bei hat jedoch jede andere Wahl die Form y+f(w) für geeignetes $w\in A$ . Als Folge wird durch z+a(w) ersetzt, was dann jedoch auf denselben Wert für d(x) führt. Somit ist die Abbildung wohldefiniert.

Hat man zu $x_{1},x_{2}\in \operatorname {ker}(c)$ jeweils $y_{1},y_{2}\in B$ sowie $z_{1},z_{2}\in A'$ mit $g(y_{{1,2}})=x_{{1,2}}$ und $f'(z_{{1,2}})=b(y_{{1,2}})$ gewählt, so kann man zu $x_{1}+x_{2}$ offenbar $y_{1}+y_{2}$ sowie $z_{1}+z_{2}$ wählen: $g(y_{1}+y_{2})=x_{1}+x_{2}$ , $f'(z_{1}+z_{2})=b(y_{1}+y_{2})$ . Hieraus ergibt sich $d(x_{1}+x_{2})=d(x_{1})+d(x_{2})$ . Ebenso folgt, wenn ein Ringelement ist, aus $g(r\cdot y_1)=r\cdot x_1$ und $f'(r\cdot z_{1})=b(r\cdot y_{1})$ , dass $d(r\cdot x_{1})=r\cdot d(x_{1})$ ist. Somit ist die Abbildung linear, also ein Homomorphismus.

Komplexeigenschaft

Dass die Schlangensequenz einen Komplex bildet, dass also zwei „Pfeile“ hintereinander stets die Nullabbildung ergeben, folgt rasch:

Die Abbildung $\ker a\to \ker c$ wird induziert von $g\circ f=0$
Für die Abbildung $\ker b\to \operatorname {coker}a$ sei $y\in \ker b$ und . Dann kann man in der obigen Konstruktion von ebendieses wählen, woraus sich , dann und somit ergibt.
Für die Abbildung $\ker c\to \operatorname {coker}b$ sei $x\in \ker c$ . Mit den Bezeichnungen wie in der Konstruktion oben ergibt sich das Bild in $\operatorname {coker}b$ aus $b(y)\in B'$ . Da dies in $\operatorname {Bild}b$ liegt, ergibt sich 0.
Die Abbildung $\operatorname {coker}a\to \operatorname {coker}c$ wird induziert von $g'\circ f'=0$

Exaktheit

Die Exaktheit der Homomorphismen zwischen den Kernen, zwischen den Kokernen sowie an Anfangs- und Endpunkt des Pfeils d weist man wiederum durch Diagrammjagd nach:

Exaktheit bei $\ker b$ : Ist $x\in \ker b$ mit , so immerhin für ein $u\in A$ . Wegen und der Injektivität von folgt , also in der Tat wie erforderlich für ein $u\in \ker a$ .
Exaktheit bei $\ker c$ : Sei $x\in \ker c$ mit . Mit den Bezeichnungen von oben ist dann für ein $u\in A$ . Dann ist , folglich für ein $v\in \ker b$ . Damit wird
Exaktheit bei $\operatorname {coker}a$ : Ein Element ${\bar {z}}$ von $\operatorname {coker}a$ stammt stets von einem $z\in A'$ . Dass es auf $0\in \operatorname {coker}b$ abgebildet wird, bedeutet, dass im Bild von liegt. Sei $y\in B$ mit und setze . Dann gilt . Somit ist $x\in \ker c$ und es wird, so wie es nach Konstruktion auf das gegebene ${\bar {z}}$ abgebildet.
Exaktheit bei $\operatorname {coker}b$ : Ist ${\bar x}\in \operatorname {coker}b$ $x\in B'$ und wird ${\bar {x}}$ auf die Null in $\operatorname {coker}c$ abgebildet, so gilt für ein $y\in C$ . Wegen der Surjektivität von gibt es ein $z\in B$ mit . Dann , also für ein $u\in A'$ . Beim Übergang zu den Kokernen fällt weg, also ist ${\bar {x}}$ das Bild von ${\bar u}\in \operatorname {coker}a$ .

Die letzten drei Punkte nutzen aus, dass die vertikalen Sequenzen exakt sind.

Natürlichkeit

Für Anwendungen des Schlangenlemmas ist es häufig nötig, dass die langen exakten Sequenzen „natürlich“ sind (im Sinne einer natürlichen Transformation). Dies ergibt sich dann aus der Natürlichkeit der vom Schlangenlemma gelieferten Sequenz.

Ist

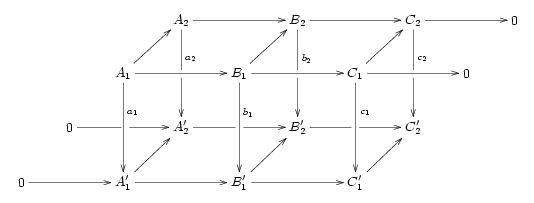
Snake lemma nat.png

ein kommutatives Diagramm mit exakten Zeilen, so kann man das Schlangenlemma einmal auf den "vorderen" Teil anwenden und einmal auf den "hinteren". Die beiden sich ergebenden exakten Sequenzen stehen miteinander über ein Diagramm der Form

Snake lemma nat2.svg

in Beziehung.

Man kann dies auch durch Anwendung des Schlangenlemmas auf die Kategorie der Morphismen zwischen Objekten der ursprünglichen Kategorie erkennen.

Kategorie der Gruppen

Da eine Reihe von Sätzen der homologischen Algebra nicht nur für abelsche Kategorien, sondern auch für die Kategorie der Gruppen Gültigkeit haben, sei darauf hingewiesen, dass dies für das Schlangenlemma nicht der Fall ist. Zwar findet man auch hier einen natürlichen Verbindungshomomorphismus d, jedoch ist die lange Folge lediglich ein Kettenkomplex und nicht notwendigerweise exakt. Nur wenn die vertikalen Sequenzen exakt sind, d.h. die Bilder unter a, b und c jeweils Normalteiler in A, B bzw.C sind, funktioniert der Beweis der Exaktheit auch für Gruppen.

Die einfache alternierende Gruppe A_5 enthält eine zur symmetrischen Gruppe $S_{3}$ isomorphe Untergruppe, in der wiederum die zyklische Gruppe $C_{3}$ ein Normalteiler ist. Hieraus erhält man ein kommutatives Diagramm

${\begin{matrix}&0&\to &C_{3}&\to &C_{3}&\to 0\\&\downarrow &&\downarrow &&\downarrow \\0\to &0&\to &S_{3}&\to &A_{5}\end{matrix}}$

mit exakten Zeilen.

Da A_5 einfach ist, ist der Kokern der rechten Abbildung trivial, während $S_{3}/C_{3}$ isomorph zu $C_{2}$ ist. Die lange Sequenz hat daher die Form

$0\longrightarrow 0\longrightarrow 0\longrightarrow 0\longrightarrow C_{2}\longrightarrow 0$

und ist folglich nicht exakt.

Basierend auf einem Artikel in:

Wikipedia.de