
Mengenlehre
Die Mengenlehre ist ein grundlegendes Teilgebiet der Mathematik, das sich mit der Untersuchung von Mengen, also von Zusammenfassungen von Objekten, beschäftigt. Die gesamte Mathematik, wie sie heute üblicherweise gelehrt wird, ist in der Sprache der Mengenlehre formuliert und baut auf den Axiomen der Mengenlehre auf. Die meisten mathematischen Objekte, die in Teilbereichen wie Algebra, Analysis, Geometrie, Stochastik oder Topologie behandelt werden, um nur einige wenige zu nennen, lassen sich als Mengen definieren. Gemessen daran ist die Mengenlehre eine recht junge Wissenschaft; erst nach der Überwindung der Grundlagenkrise der Mathematik im frühen 20. Jahrhundert konnte die Mengenlehre ihren heutigen, zentralen und grundlegenden Platz in der Mathematik einnehmen.
Geschichte
19. Jahrhundert
Die Mengenlehre wurde von Georg Cantor in den Jahren 1874 bis 1897 begründet. Statt des Begriffs Menge benutzte er anfangs Wörter wie „Inbegriff“ oder „Mannigfaltigkeit“; von Mengen und Mengenlehre sprach er erst später. 1895 formulierte er folgende Mengendefinition:
„Unter einer ‚Menge‘ verstehen wir jede Zusammenfassung M von bestimmten wohlunterschiedenen Objekten m unserer Anschauung oder unseres Denkens (welche die ‚Elemente‘ von M genannt werden) zu einem Ganzen.“
Cantor klassifizierte die Mengen, insbesondere die unendlichen, nach ihrer Mächtigkeit. Für endliche Mengen ist das die Anzahl ihrer Elemente. Er nannte zwei Mengen gleichmächtig, wenn sie sich bijektiv aufeinander abbilden lassen, das heißt, wenn es eine Eins-zu-eins-Beziehung zwischen ihren Elementen gibt. Die so definierte Gleichmächtigkeit ist eine Äquivalenzrelation und die Mächtigkeit oder Kardinalzahl einer Menge M ist nach Cantor die Äquivalenzklasse der zu M gleichmächtigen Mengen. Er beobachtete wohl als Erster, dass es verschiedene unendliche Mächtigkeiten gibt. Die Menge der natürlichen Zahlen und alle dazu gleichmächtigen Mengen heißen nach Cantor abzählbar, alle anderen unendlichen Mengen heißen überabzählbar.
- Wichtige Ergebnisse von Cantor
- Die Mengen der natürlichen, der rationalen (Cantors erstes Diagonalargument) und der algebraischen Zahlen sind abzählbar und damit gleichmächtig.
- Die Menge der reellen Zahlen hat größere Mächtigkeit als die der natürlichen Zahlen, ist also nichtabzählbar (Cantors zweites Diagonalargument).
- Die Menge aller Untermengen einer Menge M (ihre Potenzmenge) hat stets größere Mächtigkeit als M, das ist auch als Satz von Cantor bekannt.
- Von je zwei Mengen ist mindestens eine gleichmächtig zu einer Untermenge der anderen. Das wird mit Hilfe der von Cantor ausführlich behandelten Wohlordnung bewiesen.
- Es gibt überabzählbar viele Mächtigkeiten.
Cantor benannte das Kontinuumproblem: „Gibt es eine Mächtigkeit zwischen derjenigen der Menge der natürlichen Zahlen und derjenigen der Menge der reellen Zahlen?“ Er selbst versuchte es zu lösen, blieb aber erfolglos. Später stellte sich heraus, dass die Frage grundsätzlich nicht entscheidbar ist.
Neben Cantor war auch Richard Dedekind ein wichtiger Wegbereiter der Mengenlehre. Er sprach von Systemen statt von Mengen und entwickelte 1872 eine mengentheoretische Konstruktion der reellen Zahlen und 1888 eine verbale mengentheoretische Axiomatisierung der natürlichen Zahlen. Er formulierte hier als erster das Extensionalitätsaxiom der Mengenlehre.
Giuseppe Peano, der
Mengen als Klassen bezeichnete, schuf bereits 1889 den ersten formalen Klassenlogik-Kalkül als
Basis für seine Arithmetik mit den Peano-Axiomen,
die er erstmals in einer präzisen mengentheoretischen Sprache formulierte. Er
entwickelte damit die Grundlage für die heutige Formelsprache der Mengenlehre
und führte viele heute gebräuchliche Symbole ein, vor allem das Elementzeichen ,
das als „ist Element von“ verbalisiert wird. Dabei
ist
der kleine Anfangsbuchstabe ε (Epsilon)
des Wortes ἐστί
(griechisch „ist“).
Eine andere mengentheoretische Begründung der Arithmetik versuchte Gottlob Frege wenig später in seinem Kalkül von 1893. In diesem entdeckte Bertrand Russell 1902 einen Widerspruch, der als Russellsche Antinomie bekannt wurde. Dieser Widerspruch und auch andere Widersprüche entstehen aufgrund einer uneingeschränkten Mengenbildung, weshalb die Frühform der Mengenlehre später als naive Mengenlehre bezeichnet wurde. Cantors Mengendefinition beabsichtigt aber keine solche naive Mengenlehre, wie sein Beweis der Allklasse als Nichtmenge durch die zweite Cantorsche Antinomie belegt.
Cantors Mengenlehre wurde von seinen Zeitgenossen in ihrer Bedeutung kaum erkannt und keineswegs als revolutionärer Fortschritt angesehen, sondern stieß bei manchen Mathematikern, etwa bei Leopold Kronecker, auf Ablehnung. Noch mehr geriet sie in Misskredit, als Antinomien bekannt wurden, so dass etwa Henri Poincaré spottete: „Die Logik ist gar nicht mehr steril – sie zeugt jetzt Widersprüche.“
20. Jahrhundert
Im 20. Jahrhundert setzten sich Cantors Ideen immer mehr durch; gleichzeitig vollzog sich innerhalb der sich entwickelnden Mathematischen Logik eine Axiomatisierung der Mengenlehre, mittels derer zuvor herrschende Widersprüche überwunden werden konnten.
1903/1908 entwickelte Bertrand Russell seine Typentheorie, in der Mengen stets einen höheren Typ als ihre Elemente haben, damit problematische Mengenbildungen unmöglich würden. Er wies den ersten Ausweg aus den Widersprüchen und zeigte in den Principia Mathematica von 1910–1913 auch ein Stück der Leistungsfähigkeit der angewandten Typentheorie. Letztlich erwies sie sich aber als unzulänglich für Cantors Mengenlehre und konnte sich auch wegen ihrer Kompliziertheit nicht durchsetzen.
Handlicher und erfolgreicher war dagegen die von Ernst Zermelo 1907 entwickelte axiomatische Mengenlehre, die er gezielt zur widerspruchsfreien Begründung der Mengenlehre von Cantor und Dedekind schuf. Abraham Fraenkel bemerkte 1921, dass dazu zusätzlich sein Ersetzungsaxiom nötig sei. Zermelo fügte es in sein Zermelo-Fraenkel-System von 1930 ein, das er kurz ZF-System nannte. Er konzipierte es auch für Urelemente, die keine Mengen sind, aber als Mengenelemente in Frage kommen und Cantors „Objekte unserer Anschauung“ einkalkulieren. Die heutige Zermelo-Fraenkel-Mengenlehre ist dagegen nach Fraenkels Vorstellung eine reine Mengenlehre, deren Objekte ausschließlich Mengen sind.
Viele Mathematiker setzten aber statt auf eine konsequente Axiomatisierung auf eine pragmatische Mengenlehre, die Problem-Mengen mied, so etwa die oft aufgelegten Mengenlehren von Felix Hausdorff ab 1914 oder von Erich Kamke ab 1928. Nach und nach wurde es immer mehr Mathematikern bewusst, dass die Mengenlehre eine unentbehrliche Grundlage für die Strukturierung der Mathematik ist. Das ZF-System bewährte sich in der Praxis, weshalb es heute als Basis der modernen Mathematik von der Mehrheit der Mathematiker anerkannt ist; keinerlei Widersprüche konnten mehr aus dem ZF-System abgeleitet werden. Die Widerspruchsfreiheit konnte allerdings nur für die Mengenlehre mit endlichen Mengen nachgewiesen werden, aber nicht für das komplette ZF-System, das Cantors Mengenlehre mit unendlichen Mengen enthält; nach Gödels Unvollständigkeitssatz von 1931 ist ein solcher Nachweis der Widerspruchsfreiheit prinzipiell nicht möglich. Gödels Entdeckungen steckten nur Hilberts Programm, die Mathematik und Mengenlehre auf eine nachweislich widerspruchsfreie axiomatische Basis zu stellen, eine Grenze, aber hinderten den Erfolg der Mengenlehre in keiner Weise, so dass von einer Grundlagenkrise der Mathematik, von der Anhänger des Intuitionismus sprachen, in Wirklichkeit nichts zu spüren war.
Die endgültige Anerkennung der ZF-Mengenlehre in der Praxis zog sich allerdings noch über längere Zeit hin. Die Mathematiker-Gruppe mit Pseudonym Nicolas Bourbaki trug wesentlich zu dieser Anerkennung bei; sie wollte die Mathematik auf Basis der Mengenlehre einheitlich neu darstellen und setzte dies ab 1939 in zentralen Mathematikgebieten erfolgreich um. In den 1960er Jahren wurde es dann allgemein bekannt, dass sich die ZF-Mengenlehre als Grundlage der Mathematik eignet. Es gab sogar einen vorübergehenden Zeitraum, in dem die Mengenlehre in der Grundschule behandelt wurde.
Parallel zur Erfolgsgeschichte der Mengenlehre blieb jedoch die Diskussion der Mengenaxiome in der Fachwelt aktuell. Es entstanden auch alternative axiomatische Mengenlehren, etwa 1937 die sich nicht an Cantor oder Zermelo-Fraenkel, sondern an der Typentheorie orientierende Mengenlehre von Willard Van Orman Quine aus dessen New Foundations (NF), 1940 die Neumann-Bernays-Gödel-Mengenlehre, die ZF auf Klassen verallgemeinert, oder 1955 die Ackermann-Mengenlehre, die neu an Cantors Mengendefinition anknüpfte.
Definitionen
In der reinen Mengenlehre ist das Elementprädikat
(sprich ist Element von) die einzige notwendige Grundrelation. Alle
mengentheoretischen Begriffe und Aussagen werden aus ihr mit logischen
Operatoren der Prädikatenlogik
definiert.
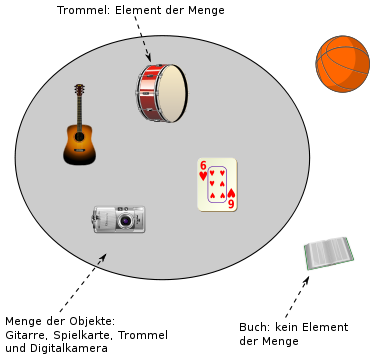
- Aufzählende Notation
- Die Elemente einer Menge werden durch die Mengenklammern { und } zu einem Ganzen, der Menge, zusammengefasst.
- Die Menge, welche aus den Elementen
bis
besteht, enthält das Element
genau dann, wenn
mit einem der
übereinstimmt. Formal:
- Z.B. ist die Aussage
- äquivalent zur Aussage
- Beschreibende Notation
- Die Menge der
, für die das Prädikat
gilt, enthält ein Element
genau dann, wenn das Prädikat auf
zutrifft. Formal:
- Zu dieser unbeschränkten Beschreibung gibt es auch eine beschränkte
Variante:
- Oft kommt auch die Kurzschreibweise
- vor, wobei mit
ein Funktionsterm gemeint ist.
- Entsprechend der Definition der Gleichheit von zwei Mengen lässt sich die
Aussage
- jetzt in den logischen Ausdruck
- auflösen.
- Teilmenge
-
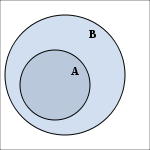
ist eine (echte) Teilmenge von
-
→ Hauptartikel: Teilmenge
- Eine Menge
heißt Teilmenge einer Menge
, wenn jedes Element von
auch Element von
ist. Formal:
- Leere Menge
-
→ Hauptartikel: Leere Menge
- Die Menge, die kein Element enthält, heißt leere Menge. Sie wird mit
oder auch
bezeichnet.
- Für die Negation
schreibt man kürzer
.
- Schnittmenge
-
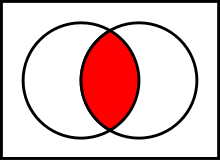 Schnittmenge von
Schnittmenge vonund
- Gegeben ist eine nichtleere Menge
von Mengen. Die Schnittmenge (auch Durchschnittsmenge) von
ist die Menge der Objekte, die in jedem Element von
– das ist jeweils wiederum eine Menge – enthalten sind. Formal:
- Vereinigungsmenge
-
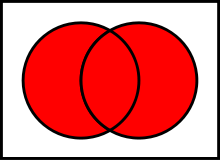 Vereinigungsmenge von
Vereinigungsmenge vonund
- Dies ist der zur Schnittmenge duale
Begriff: Die Vereinigungsmenge einer (nicht notwendigerweise nichtleeren)
Menge
von Mengen ist die Menge der Objekte, die in mindestens einem Element von
enthalten sind. Formal:
- Gleichheit von Mengen
- Zwei Mengen heißen gleich, wenn sie dieselben Elemente enthalten.
- Diese Definition bezeichnet die Extensionalität
und damit die grundlegende Eigenschaft von Mengen. Formal:
- Differenz und Komplement
-
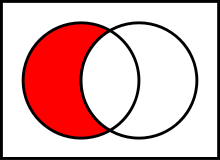
ohne
- Die Differenz wird gewöhnlich nur für zwei Mengen definiert: Die
Differenzmenge (auch Restmenge) von
und
(umgangssprachlich auch A ohne B, s. Abb.) ist die Menge der Elemente, die in
, aber nicht in
enthalten sind. Formal:
- Man nennt die Differenz auch Komplement von B in Bezug auf A. Ist
die Menge A als Grundmenge vorausgesetzt und B eine Teilmenge
von A, spricht man einfach vom Komplement der Menge B und schreibt
z.B.:
- Symmetrische Differenz
-
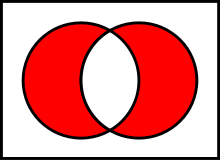 Symmetrische Differenz von
Symmetrische Differenz vonund
- Bisweilen wird noch die „symmetrische Differenz“ benötigt:
- Potenzmenge
-
→ Hauptartikel: Potenzmenge
- Die Potenzmenge
einer Menge
ist die Menge aller Teilmengen von
.
- Die Potenzmenge einer Menge
enthält immer die leere Menge und die Menge
selbst. Somit ist
, also eine einelementige Menge.
- Geordnetes Paar
Auch der Begriff des geordneten
Paares wird auf
zurückgeführt. Nach Kuratowski
geschieht dies in zwei Schritten:
- Zweiermenge:
- Geordnetes Paar:
- Kartesisches Produkt
- Die Produktmenge oder das kartesische Produkt, in älterer Terminologie auch Verbindungsmenge oder Produkt zweiter Art, soll hier ebenfalls zunächst als Verknüpfung von zwei Mengen definiert werden:
- Die Produktmenge von
und
ist die Menge aller geordneten Paare, deren erstes Element aus
und deren zweites Element aus
ist.
- Relationen und Funktionen
- Eine Relation
zwischen
und
ist eine Teilmenge
.
- Eine Funktion
von
nach
, in Zeichen
, ist eine Relation
mit
(d.h. zu jedem
gibt es mindestens einen Funktionswert)
(d.h. zu jedem
gibt es höchstens einen Funktionswert).
- Für
schreibt man suggestiver
. Damit sind auch diese Begriffe auf die
-Beziehung zurückgeführt. Damit lassen sich weitere Begriffe wie Äquivalenzrelation, injektive Funktion, surjektive Funktion, bijektive Funktion und vieles mehr definieren.
- Quotientenmenge
- Ist eine Äquivalenzrelation
gegeben, lässt sich zunächst die Äquivalenzklasse eines Elements
definieren:
- Die Menge aller Äquivalenzklassen wird Quotientenmenge genannt:
- Sagt die Äquivalenzrelation z.B. aus, dass zwei Schüler in dieselbe Klasse gehen, dann ist die Äquivalenzklasse eines Schülers seine Schulklasse und die Quotientenmenge die Menge der Schulklassen der Schule.
- Natürliche Zahlen
Nach John von Neumann kann man die natürlichen Zahlen in der Mengenlehre wie folgt definieren:
Damit sollte klar sein, wie man mittels obiger Definitionen alle weiteren Begriffe der Mathematik auf den Mengenbegriff zurückführen kann.
- Mächtigkeit und Kardinalzahl
- Mit den Begriffen der bijektiven Funktion und der Äquivalenzrelation lässt
sich nun auch die eingangs erwähnte Mächtigkeit
einer Menge definieren. Die Mächtigkeit oder Kardinalität einer Menge
wird mit
(zuweilen auch #
) bezeichnet. Eine Menge heißt endlich, wenn sie gleichmächtig zu einer natürlichen Zahl ist, dann ist
die Anzahl der Elemente von
. Damit ist der Begriff Kardinalzahl eine Verallgemeinerung der Elementanzahl einer (endlichen) Menge. Unter Einbeziehung der Arithmetik der Kardinalzahlen wird die Mächtigkeit der Potenzmenge von
, auch bei unendlichen Mengen, mit
bezeichnet.
Gesetzmäßigkeiten
Die Menge
ist bezüglich der Relation
partiell
geordnet, denn für alle
gilt:
- Reflexivität:
- Antisymmetrie:
Aus
und
folgt
- Transitivität:
Aus
und
folgt
Die Mengen-Operationen Schnitt
und Vereinigung
sind kommutativ, assoziativ und zueinander distributiv:
- Assoziativgesetz:
und
- Kommutativgesetz:
und
- Distributivgesetz:
und
- De
Morgansche Gesetze:
und
- Absorptionsgesetz:
und
Für die Differenzmenge gelten folgende Gesetzmäßigkeiten:
- Assoziativgesetze:
und
- Distributivgesetze:
und
und
und
Für die symmetrische Differenz gelten folgende Gesetzmäßigkeiten:
- Assoziativgesetz:
- Kommutativgesetz:
- Distributivgesetz:
Siehe auch
Literatur
- Felix Hausdorff: Grundzüge der Mengenlehre. Chelsea Publ. Co., New York 1914/1949/1965, ISBN 978-3-540-42224-2.
- Adolf Fraenkel: Einleitung in die Mengenlehre. Springer, Berlin / Heidelberg / New York, NY 1928. Neudruck: Martin Sändig oHG, Walluf 1972, ISBN 3-500-24960-4.
- Arnold Oberschelp: Allgemeine Mengenlehre. BI-Wissenschaft, Mannheim / Leipzig / Wien / Zürich 1994, ISBN 3-411-17271-1.
- Heinz-Dieter Ebbinghaus: Einführung in die Mengenlehre. Spektrum Akademischer Verlag, Heidelberg / Berlin 2003, ISBN 3-8274-1411-3.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 27.09. 2025