Pyramide (Geometrie)

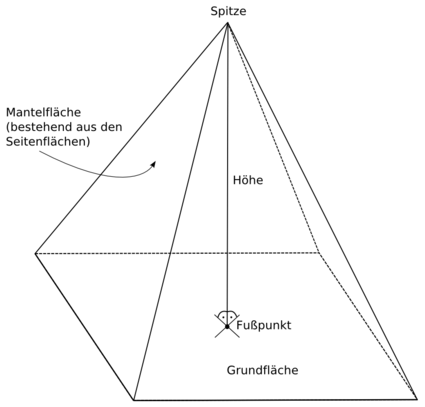
Die Pyramide ist ein geometrischer Körper, genauer ein Polyeder, dessen Grundfläche ein Polygon ist und dessen Seitenflächen Dreiecke sind, die einerseits dem Polygon benachbart sind und die sich andererseits in einem Punkt, der sogenannten Spitze der Pyramide, treffen. Das Polygon heißt auch Grundfläche der Pyramide. Die Dreiecke bilden zusammen die Mantelfläche der Pyramide.

Konstruktion

Von einem ausgezeichneten Punkt, der Pyramidenspitze, geht ein Strahlenbüschel aus, dessen Strahlen eine Ebene in den Eckpunkten der Grundfläche der Pyramide schneiden. Mit vier Strahlen einer bestimmten Neigung im Raum erhält man beispielsweise eine quadratische Grundfläche und bildet so die Quadratpyramide. Man kann die Konstruktion auch mit einer beliebigen Grundfläche eines Polygons der Ebene beginnen und einen Punkt außerhalb dieser Ebene wählen, der dann die Pyramidenspitze wird. Indem man jeden Eckpunkt der Grundfläche mit der Spitze verbindet, entsteht das erwähnte Strahlenbüschel. Die Punkte jeder einzelnen Grundflächenkante sind über die Dreiecksfläche mit der Pyramidenspitze verbunden. Damit erfüllt die Pyramide auch die Definition eines Kegels.

Eigenschaften

Hat die Grundfläche einer Pyramide Ecken so ist die Anzahl der dreieckigen Seitenflächen ebenfalls gleich Zusammen mit der Grundfläche hat die Pyramide dann insgesamt n+1 Flächen. Die Zahl der Ecken ist ebenfalls $n+1,$ nämlich Ecken in der Grundfläche zuzüglich der Spitze. Die Grundfläche enthält Kanten. Zusammen mit den ebenso vielen Seitenlinien des Strahlenbüschels, die die Ecken der Grundfläche mit der Pyramidenspitze verbinden, hat die Pyramide insgesamt also $2\cdot n$ Kanten. Diese Zählung bestätigt für den Fall der Pyramide den eulerschen Polyedersatz über die Anzahl der Ecken, der Anzahl der Kanten und der Anzahl der Flächen eines Polyeders:

$E-K+F=(n+1)-2\cdot n+(n+1)=2$

Für die Berechnung des Volumens ist der Begriff der Höhe einer Pyramide von Bedeutung. Man versteht darunter den Abstand der Pyramidenspitze von der Ebene, in der die Grundfläche liegt.

Der Schwerpunkt einer Pyramide liegt auf der Verbindungsstrecke zwischen dem Schwerpunkt der Grundfläche und der Pyramidenspitze. Er teilt diese Strecke im Verhältnis 1 : 3 und hat daher den Abstand ${\tfrac {h}{4}}$ von der Grundflächen-Ebene.

Regelmäßige Pyramide

Eine Pyramide, deren Grundfläche ein gleichseitiges Dreieck ist und deren drei Seitenflächen zur Grundfläche kongruente Dreiecke sind, nennt man regelmäßiges Tetraeder.

Eine Pyramide, deren Grundfläche ein Quadrat ist und deren Pyramidenspitze senkrecht über dem Mittelpunkt der Grundfläche liegt, heißt quadratische Pyramide.

Tetraeder und quadratische Pyramide sind sogenannte regelmäßige oder reguläre Pyramiden. Von einer regelmäßigen oder regulären Pyramide spricht man, wenn die Grundfläche der Pyramide ein regelmäßiges Polygon ist und der Mittelpunkt dieses Polygons zugleich der Fußpunkt der Pyramidenhöhe ist. Die anderen Seitenflächen sind daher gleichschenklige Dreiecke. Jede regelmäßige Pyramide ist daher auch gerade (siehe Abschnitt Gerade Pyramide).

Eine regelmäßige Pyramide ist durch drei Bestimmungsstücke vollständig bestimmt, zum Beispiel, wenn die Anzahl der Ecken/Kanten der Grundfläche, die Seitenlänge der Grundfläche und die Höhe gegeben ist.

Tetraeder
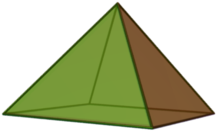Quadratische Pyramide
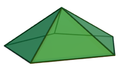Regelmäßige fünfseitige Pyramide
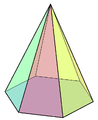Regelmäßige sechsseitige Pyramide

Formeln

Größen einer regelmäßigen Pyramide (regelmäßiges n-Eck mit Seitenlänge a als Grundfläche und Höhe h)
	Allgemeiner Fall	Quadratische Pyramide	Regelmäßige Dreieckspyramide
Volumen	$V={\frac {n\cdot a^{2}\cdot h}{12}}\cdot \cot \left({\frac {\pi }{n}}\right)$	$V={\frac {a^{2}\cdot h}{3}}$	$V={\frac {a^{2}\cdot h}{12}}\cdot {\sqrt {3}}$
Oberflächeninhalt	$O={\frac {n\cdot a}{4}}\cdot \left(a\cdot \cot \left({\frac {\pi }{n}}\right)+{\sqrt {4\cdot h^{2}+a^{2}\cdot \cot ^{2}\left({\frac {\pi }{n}}\right)}}\right)$	$O=a^{2}+a\cdot {\sqrt {4\cdot h^{2}+a^{2}}}$	$O={\frac {3\cdot a}{4}}\cdot \left({\frac {a}{3}}\cdot {\sqrt {3}}+{\sqrt {4\cdot h^{2}+{\frac {a^{2}}{3}}}}\right)$
Steilkantenlänge	$l=\left(h^{2}+{\frac {a^{2}}{4\cdot \sin ^{2}\left({\frac {\pi }{n}}\right)}}\right)^{\frac {1}{2}}$	$l={\sqrt {h^{2}+{\frac {a^{2}}{2}}}}$	$l={\sqrt {h^{2}+{\frac {a^{2}}{3}}}}$
Umkugelradius	$r_{u}={\frac {h}{2}}+{\frac {a^{2}}{8\cdot h\cdot \sin ^{2}\left({\frac {\pi }{n}}\right)}}$	$r_{u}={\frac {h}{2}}+{\frac {a^{2}}{4\cdot h}}$	$r_{u}={\frac {h}{2}}+{\frac {a^{2}}{6\cdot h}}$
Inkugelradius	$r_{i}={\frac {a\cdot h}{a+{\sqrt {4\cdot h^{2}\cdot \tan ^{2}\left({\frac {\pi }{n}}\right)+a^{2}}}}}$	$r_{i}={\frac {a\cdot h}{a+{\sqrt {4\cdot h^{2}+a^{2}}}}}$	$r_{i}={\frac {a\cdot h}{a+{\sqrt {12\cdot h^{2}+a^{2}}}}}$
Innenwinkel der regelmäßigen Grundfläche	$\alpha ={\frac {n-2}{n}}\cdot 180^{\circ }$	$\alpha =90^{\circ }$	$\alpha = 60^\circ$
Basiswinkel der gleichschenkligen Dreiecke	$\alpha _{1}=\alpha _{2}=\arctan \left({\frac {1}{a}}\cdot {\sqrt {4\cdot h^{2}+a^{2}\cdot \cot ^{2}\left({\frac {\pi }{n}}\right)}}\right)$	$\alpha _{1}=\alpha _{2}=\arctan \left({\frac {1}{a}}\cdot {\sqrt {4\cdot h^{2}+a^{2}}}\right)$	$\alpha _{1}=\alpha _{2}=\arctan \left({\frac {1}{a}}\cdot {\sqrt {4\cdot h^{2}+{\frac {a^{2}}{3}}}}\right)$
Winkel an der Spitze der gleichschenkligen Dreiecke	$\alpha _{3}=2\cdot \arctan \left({\frac {a}{\sqrt {4\cdot h^{2}+a^{2}\cdot \cot ^{2}\left({\frac {\pi }{n}}\right)}}}\right)$	$\alpha _{3}=2\cdot \arctan \left({\frac {a}{\sqrt {4\cdot h^{2}+a^{2}}}}\right)$	$\alpha _{3}=2\cdot \arctan \left({\frac {a}{\sqrt {4\cdot h^{2}+{\frac {a^{2}}{3}}}}}\right)$
Winkel zwischen Grundfläche und gleichschenkligen Dreiecken	$\beta _{1}=\arctan \left({\frac {2\cdot h\cdot \tan \left({\frac {\pi }{n}}\right)}{a}}\right)$	$\beta _{1}=\arctan \left({\frac {2\cdot h}{a}}\right)$	$\beta _{1}=\arctan \left({\frac {2\cdot {\sqrt {3}}\cdot h}{a}}\right)$
Winkel zwischen den gleichschenkligen Dreiecken	$\beta _{2}=2\cdot \arctan \left({\frac {1}{2\cdot h}}\cdot \left({\frac {4\cdot h^{2}\cdot \sin ^{2}\left({\frac {\pi }{n}}\right)+a^{2}}{\tan ^{2}\left({\frac {\pi }{n}}\right)-\sin ^{2}\left({\frac {\pi }{n}}\right)}}\right)^{\frac {1}{2}}\right)$	$\beta _{2}=2\cdot \arctan \left({\frac {1}{2\cdot h}}\cdot {\sqrt {4\cdot h^{2}+2\cdot a^{2}}}\right)$	$\beta _{2}=2\cdot \arctan \left({\frac {1}{3\cdot h}}\cdot {\sqrt {3\cdot h^{2}+a^{2}}}\right)$
Raumwinkel an der Grundfläche	$\Omega _{1}=4\cdot \arctan \left({\sqrt {\tan \left({\frac {2\cdot \beta _{1}+\beta _{2}}{4}}\right)\cdot \tan \left({\frac {2\cdot \beta _{1}-\beta _{2}}{4}}\right)\cdot \tan ^{2}\left({\frac {\beta _{2}}{4}}\right)}}\right)$
Raumwinkel in der Spitze	$\Omega _{2}=2\cdot \pi -2\cdot n\cdot \arcsin \left(\cos \left({\frac {\pi }{n}}\right)\cdot {\sqrt {\tan ^{2}\left({\frac {\pi }{n}}\right)-\tan ^{2}\left({\frac {\alpha _{3}}{2}}\right)}}\right)$

Spezialfälle

Für bestimmte Werte von und ergeben sich Zusammenhänge mit platonischen Körpern:

Für und $h={\frac {a}{3}}\cdot {\sqrt {6}}$ ergibt sich das regelmäßige Tetraeder.
Für und $h={\frac {a}{2}}\cdot {\sqrt {2}}$ ergibt sich eine quadratische Pyramide, die eine Hälfte des Oktaeders ist.
Für und $h={\frac {a}{10}}\cdot {\sqrt {50-10\cdot {\sqrt {5}}}}$ ergibt sich eine regelmäßige fünfseitige Pyramide, die ein Teil des Ikosaeders ist.

Gerade Pyramide

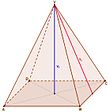
Ist die Spitze einer Pyramide über ihrer Grundfläche so positioniert, dass die Silhouette einem Beobachter, der sich in der Ebene der Grundfläche befindet, aus möglichst vielen Blickrichtungen als gleichschenkliges Dreieck erscheint, so heißt sie gerade.

Ist die Grundfläche drehsymmetrisch, dann fällt bei geraden Pyramiden der Lotfußpunkt mit dem Symmetriezentrum bzw. Schwerpunkt der Grundfläche zusammen. Ist die Grundfläche nicht nur drehsymmetrisch, sondern zusätzlich ein regelmäßiges Polygon, dann sind alle Seitenkanten, d. h. alle Kanten, die von der Spitze ausgehen, gleich lang.

Bei einer geraden Pyramide mit einem Drachenviereck als Grundfläche liegt der Fußpunkt in der Mitte der Diagonalen, welche die Symmetrieachse ist und nicht im Schnittpunkt der Diagonalen oder im Schwerpunkt.

Weist die Grundfläche einer Pyramide keinerlei Symmetrien auf, dann hat der Begriff gerade keine sinnvolle Bedeutung mehr: Ist die Grundfläche beispielsweise ein beliebiges Dreieck, so muss die Spitze der Pyramide senkrecht über seinem Umkreismittelpunkt liegen, damit alle Seitenkanten gleich lang sind. Ist dieses Dreieck weiter stumpfwinklig, dann liegt der Lotfußpunkt der Spitze sogar außerhalb der Grundfläche – was der anschaulichen Bedeutung von gerade widerspricht.

Schiefe Pyramide

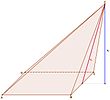
Eine Pyramide mit einem regelmäßigen Polygon als Grundfläche heißt schief, wenn nicht alle Seitenkanten gleich lang sind, sich der Fußpunkt des Lotes von der Spitze nicht im Mittelpunkt der Grundfläche befindet und daher die Verbindungsstrecke von und nicht senkrecht zur Grundfläche der Pyramide verläuft. Bei einer schiefen Pyramide kann sich daher der Fußpunkt des Lotes von der Spitze sowohl innerhalb als auch außerhalb der Pyramidengrundfläche befinden.

Johnson-Körper J₁ und J₂

Eine Quadratpyramide, deren vier dreieckige Seitenflächen gleichseitig sind, ist der einfachste Johnson-Körper, abgekürzt mit J₁. Die regelmäßige fünfseitige Pyramide, deren fünf dreieckige Seitenflächen gleichseitig sind, ist der Johnson-Körper J₂.

Quadratische Pyramide

Mantelfläche und Oberfläche

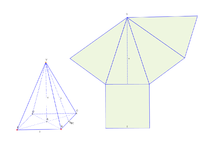
Oberfläche einer quadratischen Pyramide als Körpernetz

Die Oberfläche einer quadratischen Pyramide besteht aus der quadratischen Grundfläche und der Mantelfläche

Ist die Seitenlänge des Quadrats gegeben, ergibt sich wegen $G=a^{2}$ :

$O=a^{2}+M$

Bei einer regelmäßigen Pyramide mit quadratischer Grundfläche setzt sich die Mantelfläche aus vier Flächen kongruenter gleichschenkliger Dreiecke zusammen.

Es seien die Seitenlänge und die Pyramidenhöhe gegeben:

Die Fläche eines dieser Dreiecke ist $A_{D}={\frac {a\cdot h_{a}}{2}}$ , aller vier Flächen also $M=2\cdot a\cdot h_{a}$ . Hierbei ist $h_{a}$ die Höhe der kongruenten Seitendreiecke.

Aus dem Satz des Pythagoras ergibt sich ${h_{a}}^{2}=h^{2}+({\tfrac {a}{2}})^{2}$ . Daraus folgt $h_{a}={\sqrt {h^{2}+({\tfrac {a}{2}})^{2}}}$ und damit für die Mantelfläche $M=a\cdot {\sqrt {4\cdot h^{2}+a^{2}}}.$

Die gesamte Oberfläche beträgt somit $O=a^{2}+a\cdot {\sqrt {4\ h^{2}+a^{2}}}$ .

Steilkantenlänge

Neben den vier Grundflächenkanten besitzt die quadratische Pyramide noch vier gleich lange Steilkanten (auch Grate genannt) $AS,BS,CS$ und $DS,$ die von den Eckpunkten der Grundfläche ausgehen und nach oben ansteigend sich in der Pyramidenspitze treffen.

Es seien die Seitenlänge und die Pyramidenhöhe gegeben:

Für die Länge der Grundflächendiagonale ergibt sich aus dem Satz des Pythagoras $d^{2}=a^{2}+a^{2},$ woraus $d=a\cdot {\sqrt {2}}$ folgt.

Für die weitere Berechnung benötigt man ${\tfrac {d}{2}}={\tfrac {a}{2}}\cdot {\sqrt {2}}$ und das Quadrat davon ist ${\tfrac {a^{2}}{2}}.$

Zur Berechnung von $AS$ verwendet man wieder den Satz des Pythagoras: ${AS}^{2}=h^{2}+{\tfrac {a^{2}}{2}}$ und daraus folgt dann für den Grat $AS = \sqrt{h^2 + \tfrac{a^2}{2}}$ .

Gesamtkantenlänge

Die Gesamtkantenlänge der quadratischen Pyramide setzt sich aus den vier Seitenlängen und den vier gleich langen Graten $AS,BS,CS$ und $DS$ zusammen. Es seien wieder die Seitenlänge und die Pyramidenhöhe gegeben:

$K=4\cdot a+4\cdot {\sqrt {h^{2}+{\frac {a^{2}}{2}}}}$

$K=4\cdot \left(a+{\sqrt {h^{2}+{\frac {a^{2}}{2}}}}\right)$

Volumen als Extremwert

Papiermodell einer quadratischen Pyramide mit maximalem Volumen bei gegebener Oberfläche

Die Kugel ist ein Körper, dessen Volumen bei gegebener Oberfläche maximal ist, d.h. jede Änderung der äußeren Form würde ein kleineres Volumen ergeben. Analog haben der Würfel, das regelmäßige Tetraeder sowie das regelmäßige Oktaeder das größte Volumen unter allen Polyedern mit derselben Oberfläche und derselben Eckenzahl.

Eine quadratische Pyramide mit maximalem Rauminhalt ist hingegen vergleichsweise spitz: unter allen quadratischen Pyramiden mit derselben Oberfläche hat diejenige das größte Volumen, die $h=a\cdot {\sqrt {2}}$ hoch ist (wenn die Länge ihrer Grundseite bezeichnet). Ihr Volumen ist $V={\frac {1}{3}}\cdot a^{3}\cdot {\sqrt {2}}$ , die Dreiecke ihrer Mantelfläche sind ${\frac {3}{2}}\cdot a$ hoch.

Allgemeine Pyramide

Volumen

Das Volumen einer Pyramide errechnet sich aus dem Inhalt der Grundfläche und der Höhe gemäß

$V={\frac {1}{3}}\cdot G\cdot h.$

Diese Formel gilt für jede Pyramide. Es spielt also keine Rolle, ob die Grundfläche ein Dreieck, Viereck, Fünfeck, … ist. Die Formel ist auch gültig, wenn der Höhenfußpunkt nicht mit dem Grundflächenmittelpunkt übereinstimmt oder die Grundfläche gar keinen Mittelpunkt besitzt. Im Spezialfall einer quadratischen Pyramide ergibt sich $V = \frac{1}{3} \cdot a^2 \cdot h$ , wobei die Seitenlänge der quadratischen Grundfläche ist und die Höhe.

Die allgemeingültige Formel $V = \frac{1}{3} \cdot G \cdot h$ entspricht übrigens der Volumenformel $V={\frac {1}{3}}\cdot \pi \cdot r^{2}\cdot h$ für einen Kreiskegel. Dies liegt daran, dass jede Pyramide die Definition eines allgemeinen Kegels erfüllt. Umgekehrt kann ein Kegel auch als Pyramide mit einem regelmäßigen -Eck als Grundfläche aufgefasst werden, das nach dem Grenzübergang $n\to \infty$ zu einem Kreis entartet ist.

Berechnung mit Hilfe des Spatprodukts

Eine von den Vektoren ${\vec {a}}$ , ${\vec {b}}$ , ${\vec {c}}$ aufgespannte dreiseitige Pyramide hat das Volumen

$V={\frac {1}{6}}\cdot |({\vec {a}}\times {\vec {b}})\cdot {\vec {c}}|$ .

Elementargeometrische Begründung

Die erwähnte Volumenformel lässt sich elementargeometrisch in zwei Schritten begründen:

1. Ein Würfel kann in drei gleiche Pyramiden mit quadratischer Grundfläche zerlegt werden, deren Spitzen in einer Ecke des Würfels zusammenfallen. Die drei Grundflächen sind die drei Seitenflächen des Würfels, die diese gemeinsame Spitze nicht enthalten.

2. Zwei Pyramiden mit gleicher Grundfläche und gleicher Höhe stimmen im Volumen überein.

Zum Beweis dieser Aussage kann man das Prinzip von Cavalieri und die Gesetze der zentrischen Streckung heranziehen.

Für Pyramiden gilt demzufolge die Volumenformel $V = \frac{1}{3} \cdot G \cdot h$ .

Begründung mit Hilfe der Integralrechnung

Der Rauminhalt einer Pyramide mit der Grundfläche und Höhe kann berechnet werden, wenn man sich die Pyramide aus dünnen (infinitesimalen) Schichten der Dicke $\mathrm dy$ parallel zur Grundfläche aufgebaut vorstellt. Eine -Achse lege man nun durch die Spitze der Pyramide, sodass die Höhe mit der -Achse zusammenfällt. Bezeichnet man die Fläche der Schicht im Abstand von der Spitze mit A(y) , so kann man aus den Gesetzen der zentrischen Streckung eine Formel für A(y) herleiten:

$A(y):G=y^{2}:h^{2}$

$A(y)={\frac {G}{h^{2}}}y^{2}$

Daraus ergibt sich das Volumen der Pyramide durch Integration von y=0 bis $y=h$ nach dem Prinzip von Cavalieri:

$V=\int _{0}^{h}A(y)\,\mathrm {d} y=\int _{0}^{h}{\frac {G}{h^{2}}}y^{2}\,\mathrm {d} y={\frac {G}{h^{2}}}\int _{0}^{h}y^{2}\,\mathrm {d} y={\frac {G}{h^{2}}}\cdot {\frac {1}{3}}\left[y^{3}\right]_{0}^{h}={\frac {G}{h^{2}}}\cdot {\frac {1}{3}}\left[h^{3}-0\right]={\frac {1}{3}}G\cdot h$

Vermessung eines Pyramidenbauwerks

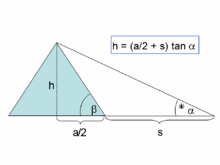
Betrachtung aus der Entfernung und Sehwinkelbestimmung in vereinfachter Form

Bei einer großen Pyramide lassen sich die Kantenlängen der Basis direkt gut vermessen, jedoch nicht die Höhe, die nicht direkt zugänglich ist. Im Folgenden sollen die grundsätzlichen Schwierigkeiten dargelegt werden, die nicht so sehr mit der Methodik des Messverfahrens selbst zusammenhängen. Ein einfaches geometrisches Verfahren zur Höhenbestimmung größerer Objekte ist die Betrachtung aus der Entfernung und die Bestimmung des Sehwinkels (in vereinfachter Form durch die nebenstehende Grafik aufgezeigt).

In einem Abstand von der unteren Pyramidenkante wird die Spitze der Pyramide unter dem gemessenen Winkel $\alpha$ angepeilt. Der Abstand des Beobachtungspunktes von der Pyramidenspitze in horizontaler Linie ist somit die halbe Grundseite $a/2+s$ . Die Höhe ergibt sich aus der Formel in der Grafik. Damit wäre die Bestimmung der Höhe kein großes Problem. Es gibt jedoch folgende Schwierigkeiten:

Die Spitze der Pyramide liegt nicht unbedingt exakt über dem Mittelpunkt der Grundfläche.
Die Länge der Basiskante der Pyramide ist nicht sauber bestimmbar (abgebrochene Steine, Erosion).
Die Spitze ist nicht mehr vorhanden (abgetragen).
Der Neigungswinkel der Pyramide ist schwer bestimmbar (Abtragung, Erosion).

Das entspricht bei den bekannten großen Pyramiden weitgehend der Realität. Die Höhenabweichung des Beobachtungspunktes, an dem $\alpha$ gemessen wird, muss genau berücksichtigt werden. Die Winkelmessung selbst kann in der Regel sehr präzise ausgeführt werden. Darüber hinaus muss definiert werden, von welchem Bodenniveau aus die Höhe der Pyramide gültig sein soll, also wo sie tatsächlich anfangen soll. Angenommen, die Basislänge der Pyramide ließe sich nicht genauer als auf 30 cm und damit die Entfernung $a/2+s$ zum Messpunkt nicht genauer als auf 15 cm bestimmen. Dadurch würde bei einem Sehwinkel $\alpha$ von angenommenen 35° die Höhe um den Betrag von etwa 10 cm ungenau sein. Es fehlt jetzt aber noch die Bestimmung des Neigungswinkels $\beta$ über die Seitenfläche. Eine hypothetische große Pyramide der Basislänge von 200 m und einer Höhe von 140 m hätte bei einer Ungenauigkeit der Höhenangabe von 10 cm eine Ungenauigkeit der Neigungswinkelangabe von etwa einer Bogenminute (54°27′44″ bei $h=140{,}0\,\mathrm {m}$ gegenüber 54°26′34″ mit $h=139{,}9\,\mathrm {m}$ ). Das gilt nun für Pyramiden, deren Spitze noch vorhanden ist. Die Realität sieht aber anders aus. Die Höhenbestimmung gibt also nicht die ursprüngliche Höhe wieder, sondern die Höhe der abgetragenen Pyramide.

Problem bei Extrapolation

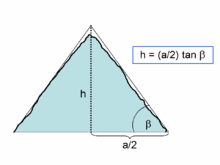
Die Spitze muss also extrapoliert werden. Das nebenstehende Bild zeigt schematisch das Problem. Sowohl die Seitenflächen als auch die Spitze sind durch Abriss und Verwitterung deutlich abgetragen:

Die Höhe wäre daher gemäß der Formel aus der direkten Bestimmung des Neigungswinkels $\beta$ zugänglich. Wie ersichtlich, ist die Bestimmung mit großen Fehlern behaftet. Eine Ausnahme bildet die Chephren-Pyramide, weil diese im oberen Teil noch die originalen Decksteine hat. Der Winkel $\beta$ ist dadurch genauer bestimmbar als bei den anderen Pyramiden. Das erklärt die gute Übereinstimmung hinsichtlich des Neigungswinkels der verschiedenen Autoren.

Damit wird klar, dass bei realen Pyramiden weder die Höhe auf den Zentimeter noch der Neigungswinkel auf die Bogensekunde exakt angegeben werden kann.