Proendliche Zahl
In der Algebra und Zahlentheorie ist eine
proendliche Zahl (auch pro-endliche Zahl, proendliche
Ganzzahl oder profinite (Ganz)zahl, englisch: profinite
integer) durch die Reste (Restklassen) festgelegt, die sie in allen
ganzzahligen Restklassenringen
bildet. Damit ist sie ein Element aus der proendlichen
Vervollständigung
(gesprochen: Zett-Dach) der Gruppe der ganzen
Zahlen
.[1][2]
Die (rationalen) Ganzzahlen
lassen sich vermöge des kanonischen injektiven Homomorphismus
in die proendlichen Zahlen einbetten. Dabei wird die Zahl
in allen Restklassenringen
auf das dortige
abgebildet. Dieses
„erzeugt“ gewissermaßen
Die so eingebetteten ganzen Zahlen
liegen dicht
in den proendlichen ganzen Zahlen
[3][4]
Sie sind in
Folgen von Restklassen, und bei den Eigenschaften bspw. einer solchen 1
oder 2 kommt es (wie häufig in der Abstrakten
Algebra) nur auf diejenigen an, die sie in ihren Verknüpfungen haben.
Die Galois-Gruppe
des algebraischen
Abschlusses eines endlichen
Körpers über diesem Körper ist isomorph
zu
Definition
Die proendliche Vervollständigung der Gruppe
der ganzen Zahlen
ist
(projektiver oder inverser Limes).
Die Bildung eines projektiven Limes erfordert ein sog. projektives
System bestehend aus einer gerichteten
Indexmenge, die eine Folge von Objekten indiziert, und Übergangsmorphismen
zwischen diesen Objekten. Für
nimmt man als gerichtete Indexmenge die natürlichen
Zahlen
die durch die Teilbarkeitsrelation
partiell
geordnet sind, und als Folge von Objekten die Folge der endlichen zyklischen Gruppen
Zu jedem
und jedem
gibt es den Gruppenhomomorphismus
(die „Restklassenabbildung“, die „natürliche Surjektion“)
der wegen
wohldefiniert
ist. Diese Homomorphismen nimmt man als Übergangsmorphismen zwischen den
Objekten. Sie bilden einen Erzeuger von
in einen von
ab und sind für
in einer Weise, nämlich
also
verträglich, wie es für das projektive System und die Bildung des projektiven Limes erforderlich ist.
Im projektiven Limes werden diejenigen Familien
von Restklassen zusammengefasst, deren Komponenten miteinander verträglich sind,
bei denen also für alle
mit
gilt:
was durch die Kongruenzen
erfüllt wird. In einer Formel geschrieben ergibt sich:
Eine Elementefamilie, die die Verträglichkeitsbedingungen
erfüllt, die also zum projektiven Limes gehört, wird manchmal auch als „Faser“
bezeichnet.
Die komponentenweise definierte Addition ist stetig. Dasselbe gilt in
zusätzlich für die Multiplikation. Dadurch wird
zu einer topologischen additiven Gruppe und zu einem topologischen Ring mit 1.
Die natürliche Topologie auf
ist die Limestopologie, d.i. die von den diskreten Topologien auf
den
induzierte Produkttopologie. Diese Topologie ist mit den Ringoperationen
verträglich und wird auch Krulltopologie
genannt. Gleichzeitig ist
die abgeschlossene
Hülle von
im Produkt
was die Dichtheit von
in
impliziert.
Alternative Konstruktion
Der Ring der ganzen Zahlen
kann auch in „klassischer“ Manier über eine uniforme
Struktur vervollständigt
werden. Sei dazu für
eine Nachbarschaft (der Ordnung ).
Die Menge
ist ein (abzählbares) Fundamentalsystem[5]
und der zugehörige Filter
eine uniforme Struktur für .
Die Forderungen an
sind leicht verifiziert:
- (1) Jede Nachbarschaft
und jedes
enthält die Diagonale
- (2) Ist
und
, dann ist
- (3) Ist
, dann ist auch
- (4) Zu jedem
gibt es ein
mit
.[6]
- (5) Ist
, dann ist auch
Die Menge
der Cauchy-Netze
in
ist
welche mit der komponentenweisen Addition eine Gruppe ist. Die
Vervollständigung der ganzen Zahlen
bezüglich der uniformen Struktur der Teilbarkeit ist die Faktorgruppe
der Cauchy-Netze modulo
den Nullfolgen
(genauer: den Folgen, die Nullnetze bzw. Cauchy-Netze mit Limes
sind).[7]
erweist sich als isomorph zu
| Beweis |
Sei
und sei
die Folge Ist umgekehrt
Nimmt man jetzt für alle
Damit erfüllt die Folge
|
- Ergebnis
- Man kann von Folgen von Restklassen
zu den Folgen ihrer Repräsentanten
übergehen – wie man auch umgekehrt aus einem Cauchy-Netz von Ganzzahlen durch Beigabe von Moduln eine Folge von Restklassen machen kann, die dieselbe proendliche Zahl ausmacht.
Eigenschaften
- Die Menge
der proendlichen Zahlen ist überabzählbar.
ist eine proendliche Gruppe.
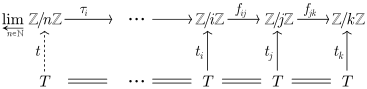
- Der projektive Limes
zusammen mit den Homomorphismen
-
- den kanonischen Projektionen (des projektiven
Limes), hat die folgende universelle
Eigenschaft:
- Für jede Gruppe
und Homomorphismen
für die
für alle
gilt, existiert ein eindeutig bestimmter Homomorphismus
so dass
gilt.
- Für jede Gruppe
isomorphismus
- Der natürliche Homomorphismus
hat die folgende universelle Eigenschaft:
-
- Für jeden Homomorphismus
in eine proendliche Gruppe
gibt es einen (bezüglich der Krulltopologie) stetigen Homomorphismus
mit
- Für jeden Homomorphismus
- Aus der eindeutigen Primfaktorzerlegung
in
folgt die Isomorphie[8]
-
- (mit
als der Menge der natürlichen Primzahlen) von
zum direkten Produkt der p-adischen Zahlringe
die ihrerseits projektive Limites
- sind.[9]
Bei der Umkehrfunktion des
Isomorphismus lässt sich zu einem beliebigen Vektor
mit Komponenten
das Urbild
(eindeutig) mithilfe des chinesischen Restsatzes bestimmen, der in einem erweiterten iterativen Verfahren, ähnlich dem im Beweis der Dichtheit im Artikel Limes (Kategorientheorie) gebrachten, angewendet wird.[10]
- Wie im projektiven Limes geschehen Addition und Multiplikation im direkten
Produkt komponentenweise. Das bedeutet, dass es Nullteiler
gibt in
und
keinen Quotientenkörper haben kann.
- Für jede Primzahl
bezeichne
- die kanonische Projektion (des direkten Produktes). Angewendet auf die Injektion
| Komponente | |||||
- erfüllt sie
Die Komposition
dagegen entspricht der Multiplikation
| | ||||||
| mit | ||||||
| | ||||||
| Komponente | ||||||
- Eine in
konvergente Zahlenfolge konvergiert auch in jedem proendlichen Unterring
und umgekehrt. Die Konvergenz für ein einzelnes
genügt allerdings nicht. Beispiel: Die Folge
die in
gegen
konvergiert, divergiert sowohl in
für Primzahlen
ungleich
wie auch in
Denn ist
die Ordnung von
in der multiplikativen Gruppe
des endlichen Körpers, dann gilt für alle
und
- Topologie
Die Produkttopologie
auf
ist die gröbste Topologie
(die Topologie mit den wenigsten offenen Mengen), bezüglich der alle
Projektionen
stetig sind.
Diese Topologie fällt mit der oben erwähnten Limestopologie zusammen und wird Krulltopologie genannt. Da der die Isomorphie etablierende Isomorphismus gleichzeitig in beiden Richtungen stetig unter den beiderseitigen Topologien ist, ist er zusätzlich ein Homöomorphismus.
Darstellung
Die Entwicklung einer proendlichen Zahl beinhaltet (wie die einer reellen) im Normalfall unendlich viele Symbole. Die solche Symbolfolgen bearbeitenden Algorithmen können davon nur endliche Anfangsstücke abarbeiten. Bei einem Abbruch ist eine Angabe über die Größenordnung des Fehlers wünschenswert, ähnlich den p-adischen Zahlen, bei denen die letzte ausgeworfene Ziffer genau ist.
Darstellung als direktes Produkt
Die Darstellung einer proendlichen Zahl
als direktes Produkt
ist ein in zwei Dimensionen unendlicher[11]
„Vektor“. Bei dieser Darstellung sind viele algebraisch-zahlentheoretiche
Eigenschaften von
anhand der Eigenschaften in den
gut erkennbar.[12]
Darstellung als unendliche Reihe
Im projektiven Limes
kann man die Halbordnung
der Teilbarkeitsrelation
durch eine lineare Ordnung
ersetzen. Sei dazu
mit
der „Stellenwert“ (das Gewicht) an der Stelle
und
mit
die „Basis“. Dann ist[13]
wobei jedes Element
eine unendliche Familie
| |
von Restklassen ist. Jeder solche Repräsentant
lässt sich als Teilsumme
| |
einer Reihe
mit „Ziffern“
in einer Stellenwertnotation
mit mehreren Basen schreiben.[14][15]
Die Indizierung ist so gewählt, dass die Ziffer
Repräsentant einer Restklasse
ist – mit einem um 1 höheren Index – und das Folgenglied
Repräsentant einer Restklasse
dem „Modul“ (an der Stelle
).[16]
| Algorithmus | ||||||||||||||||||||||||||||||||||||||||
| In der Induktionsannahme
seien für Im Induktionsschritt komme die Forderung hinzu, die für alle Teiler mit einer der kanonischen Projektionen gelten. Der erweiterte euklidische Algorithmus liefert zu den beiden Moduln Wegen was zusammengenommen ergibt. Also lässt sich bilden, so dass mit sowohl als auch gilt, wie es sein soll. ■ |
Der Algorithmus vereinigt in jedem Induktionsschritt in Anwendung des chinesischen Restsatzes (unter Zuhilfenahme des erweiterten euklidischen Algorithmus) zwei (simultane) Kongruenzen zu einer neuen, die zu den beiden Ausgangskongruenzen äquivalent ist. (Im Fall nicht-teilerfremder Moduln wird die Lösbarkeit durch die Verträglichkeitsbedingungen des projektiven Systems stets garantiert.) Das Verfahren wirft unabhängig von der Wahl des Basissystems pro Schritt ein Folgenglied einer unendlichen Reihe aus.
Werden umgekehrt Ziffern mit
frei gewählt, dann stellt die mit ihnen und dem gegebenen Basissystem
gebildete unendliche Reihe
eine (eindeutige) proendliche Zahl dar.
Kofinale Folge
Diese Reihe ist nur dann bei jedem beliebigen
eine Stellenwertentwicklung, wenn das gegebene Basissystem
jede Primzahl unendlich oft enthält, d.h. wenn die Folge der Moduln
kofinal
in
[17]
und monoton (wachsend)[18]
ist.[11]
Dies ist beim System der Fakultäten, dem A003418-
und dem A051451-basierten System der Fall. Die Monotonie vermeidet Basen
und ist wachsend, da das interessante, das offene Ende von
bei den großen Zahlen ist.
Fakultätsbasiert
Im fakultätsbasierten
Zahlensystem (engl. factorial number system) werden als Moduln die Fakultäten
[19]
und damit
als Basen gewählt. Lenstra gibt für
die Symbolfolge
- –1 = … 1010998877665544332211
- = (… 10987654321)!
und kennzeichnet sie mit dem tiefgestellten Rufzeichen. Dabei ist die Ziffer 1 ganz links wie in Lenstra Profinite Fibonacci numbers. S. 297 hochgestellt, um auszudrücken, dass sie (ggf. zusammen mit anderen hochgestellten Ziffern) bis einschließlich zur nächsten normal geschriebenen Ziffer rechts davon zu einer Dezimalzahl gehört, welche eine einzige Stelle der Darstellung ausmacht. Die Aufschreibung im Horner-Schema ist:
- = (((((((((( 10)·10+9)·9+8)·8+7)·7+6)·6+5)·5+4)·4+3)·3+2)·2+1)·1
- = 11! – 1 = 39916799 ≡ –1 (mod 39916800 = 11!).[20]
Proendliche Zahlen haben in dieser Darstellung abhängig von ihrem Rest mod 24=4·3·2 die folgenden Entwicklungen in den ersten (rechtesten) 3 Stellen:
| ≡ xx (mod 24) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | … |
| (z3 z2 z1)! | 000 | 001 | 010 | 011 | 020 | 021 | 100 | 101 | 110 | 111 | 120 | 121 | 200 | 201 | 210 | 211 | 220 | 221 | 300 | … |
Die Wahl der Fakultäten als Moduln bei der fakultätsbasierten Darstellung bevorzugt die Produkte kleiner Primfaktoren, ganz besonders des Primfaktors 2.
A003418- bzw. A051451-basiert
Die folgende Wahl der Basen und Moduln erzeugt Darstellungen, bei denen die natürlichen Zahlen umgekehrt proportional zu ihrer Größe bevorzugt werden.
Sei dazu zunächst für jedes
(kleinstes
gemeinsames Vielfaches) das Produkt der maximalen Primzahlpotenzen .[21]
In Zahlen ausgerechnet ergibt sich mit
| P:= ( | P1, | P2, | P3, | P4, | P5, | P6, | P7, | P8, | P9, | P10, | … ) |
| = ( | 1, | 1·2=2, | 2·3=6, | 6·2=12, | 12·5=60, | 60·1=60, | 60·7=420, | 420·2=840, | 840·3=2520, | 2520·1=2520, | … ) |
die Folge ![]() A003418
in OEIS.[22]
A003418
in OEIS.[22]
Wählt man für die Darstellung
als Moduln, dann sind die zugehörigen Basen
Ist
keine Primzahlpotenz, dann ist
Ist aber
eine Primzahlpotenz, etwa
dann ist
eine Primzahl.
Das Beispiel
- –1 = … 101032217610542132211
- = … 10021604121,
im Horner-Schema
- = (((((((((( 10)·1+0)·3+2)·2+1)·7+6)·1+0)·5+4)·2+1)·3+2)·2+1)·1
- = P12 – 1 = 27719 ≡ –1 (mod 27720 = P12),
gibt die Darstellung von –1 (mit nur Ziffern oder mit den Ziffern fett und den Basen normal gedruckt). Dabei ist die Ziffer 1 ganz links wie in Lenstra Profinite Fibonacci numbers. S. 297 hochgestellt, um auszudrücken, dass sie zur selben Stelle gehört wie die nächste normal geschriebene Ziffer.
Lässt man die Basen =1 zusammen mit den zu ihnen gehörenden, verschwindenden Ziffern weg, so hat man
| zu den Moduln | |||||||||
| P9=2520, | P8=840, | P7=420, | P5=60, | P4=12, | P3=6, | P2=2, | P1=1 | ||
| resp. zu den Basen | |||||||||
| b9=3, | b8=2, | b7=7, | b5=5, | b4=2, | b3=3, | b2=2 | |||
| die Entwicklung | |||||||||
| –1 | = … | 10 | 2 | 1 | 6 | 4 | 1 | 2 | 1 |
| = … | 103 | 22 | 17 | 65 | 42 | 13 | 22 | 11 | |
| = … | 10 | ·P9+ 2 | ·P8+ 1 | ·P7+ 6 | ·P5+ 4 | ·P4+ 1 | ·P3+ 2 | ·P2+ 1 | |
| = …, | 27719, | 2519, | 839, | 419, | 59, | 11, | 5, | 1 | |
| = …, | P11 – 1, | P9 – 1, | P8 – 1, | P7 – 1, | P5 – 1, | P4 – 1, | P3 – 1, | P2 – 1 | |
| ≡ –1 (mod Pn) für alle n ∈ N. | |||||||||
Die Moduln Pn dieser Darstellung machen (bei
entsprechend angepasster Indizierung) die Folge ![]() A051451 in OEIS
aus.[19]
A051451 in OEIS
aus.[19]
Unterringe
Direkte Summe
Die Elemente im direkten Produkt ,
bei denen nur endlich viele Komponenten von 0 verschieden sind, fasst man
in der direkten
Summe
zusammen. Eine proendliche Ganzzahl
dieser Art kann als
-adische
Entwicklung der Form
mit einer Basis
und Ziffern
aus
geschrieben werden. Man sagt,
wird zur Basis
notiert. Die
-Darstellung
lässt sich aus den
-Darstellungen
mit dem chinesischen
Restsatz gewinnen.
Die Darstellung ist eindeutig und kommt ohne ein vor das Literal (die
Zahlkonstante) gestelltes Vorzeichen
aus. Für alle Basen
ist
Alle diese Darstellungen zur Basis
sind dieselben wie im Ring
der ein Unterring der direkten Summe ist.[23]
Aus dieser Darstellung lässt sich erkennen, dass (zu einem )
die Basis
quadratfrei
gewählt werden kann.
Primzahlpotenzen
Für jede Primzahl
und
ist
.
| Beweis | |||||||||||||
| Eine Familie von Restklassen erfüllt für alle Kongruenzen, die trivialerweise implizieren. Daraus folgt Ist umgekehrt erfüllt. Die Familien von Restklassen sind zwar eine Vergröberung der ursprünglichen Familien. Und sie
erfüllen die Bedingungen |
Die folgende Überlegung führt zum selben Ergebnis:
Ausgehend von der -adischen
Darstellung
mit
und
kommt man über die Teilsummen
direkt zu
,
was wegen
die
-adische
Darstellung ist. Dieser Weg lässt sich auch umkehren – mit dem Ergebnis:
10-adische Zahlen
Die 10-adischen Zahlen sind ein Beispiel für einen -adischen
Ring, bei dem die Basis
keine Primzahlpotenz ist. Sie werden als projektiver Limes
gebildet und sind ein Unterring der direkten Summe.
Ultrametrik
Auf dem Ring ,
ja auf ganz
,[24]
lässt sich eine Ultrametrik
definieren, die
zu einem metrischen
Raum mit der Krulltopologie macht.
| Beweis | |||||
Eine rationale Zahl
Die Forderungen „Nicht-Negativität“ und „positive Definitheit“ aus der
Zusammenstellung Betragsfunktion#Betragsfunktion
für Körper sind leicht einzusehen. Die „Multiplikativität“ kann nicht
erfüllt werden, da
Eine solche Dreiecksungleichung nennt man verschärft. Die
mithilfe dieser Funktion ist damit eine Ultrametrik. Die von ihr induzierte Topologie stimmt mit der durch die Filter definierten überein. |
10-adisch zu 2-adisch und 5-adisch
Ist
ferner
und sind
jeweilige Repräsentanten der Nebenklassen
dann entspricht die Bedingung
der Kongruenz
Daraus folgt aber für
so dass dieselben Repräsentanten
sowohl eine proendliche 2-adische
Zahlenfolge
wie auch eine proendliche 5-adische
Zahlenfolge
ausmachen.
(2×5)-adisch zu 10-adisch
Zu frei gewählten
| und |
gibt es ein eindeutig bestimmtes >
mit
| und | |
Denn die 2 simultanen Kongruenzen
| und | |
können wegen der Teilerfremdheit der Moduln für jedes
mit dem chinesischen
Restsatz (eindeutig) gelöst werden.
wird dadurch
festgelegt.
Nullteiler
Endliche Zahlen (abbrechende Zahlfolgen) in den Ringen
und
liegen allesamt im Ring
der ganzen Zahlen. Letzterer Ring enthält bekanntlich keine Nullteiler, genauso wenig
die proendlichen Ringe
und
die ja Quotientenkörper besitzen, nämlich die 2-adischen
Zahlen
bzw. die 5-adischen Zahlen
- Beispiel 1
Wie im Abschnitt #Eigenschaften
ausgeführt, entspricht für ein
die Projektion
einer Multiplikation mit
Sind
zwei verschiedene Primzahlen, dann ist
(komponentenweise Multiplikation in
).
Das Produkt zweier proendlicher Zahlen kann also Null sein, auch wenn beide
Faktoren von Null verschieden sind.
Der Algorithmus im Abschnitt Darstellung
als unendliche Reihe liefert in
für
| zu den Stellenwerten[27] | 2520, | 840, | 420, | 60, | 12, | 6, | 2, | 1 | ||
| die A051451-Entwicklung | ||||||||||
| 12 | = … | 1 | ·P9+ 1 | ·P8+ 0 | ·P7+ 1 | ·P5+ 3 | ·P4+ 1 | ·P3+ 1 | ·P2+ 1 | |
| = …, | 3465, | 945, | 105, | 105, | 45, | 9, | 3, | 1. | ||
Die Glieder der Folge in der letzten Zeile sind ≡1 (mod 2n) und teilbar durch (im Limes immer höhere) Potenzen aller anderen Primzahlen.[28]
Für
ergibt sich die A051451-Entwicklung
| 15 | = … | 8 | ·P9+ 2 | ·P8+ 0 | ·P7+ 5 | ·P5+ 3 | ·P4+ 0 | ·P3+ 0 | ·P2+ 0 |
| = …, | 22176, | 2016, | 336, | 336, | 36, | 0, | 0, | 0 |
Die Glieder der Folge in der letzten Zeile sind ≡1 (mod 5n) und teilbar durch zunehmend höhere Potenzen aller anderen Primzahlen.
Die Folgenglieder des Produkts
sind für wachsende Indizes durch immer höhere Potenzen von 10 teilbar,
d.h. es ist Nullfolge in ganz
- Beispiel 2
Für
sei
und
.
Wegen
ist
Teiler von
.
Das bedeutet, dass die Folge
im Ring der 10-adischen Zahlen konvergiert. Ferner ist
.
Für
gilt analog:
und entsprechend
Zu jeder der beiden Folgen lässt sich eine 10-adische Entwicklung der Form
mit
mit demselben 10-adischen Limes angeben (die sich also nur um eine 10-adische
Nullfolge unterscheidet). Andererseits divergieren die Folgen für alle
Primzahlen außer 2 und 5.
Wegen
ist das Produkt
durch beliebig hohe Potenzen von 10 teilbar, so dass
in
Übrigens sind die beiden 10-adischen Zahlen Einheitswurzeln,
weil
und
zur Folge hat, dass
und
Trivialerweise ist
in
und
in
Oberringe
Der Ring der proendlichen Rationalzahlen
| |
umfasst ,
und
Außerdem ist
| | ||
| |
der Ring der endlichen Adele.[29]
Das Produkt
ist der Ring der ganzzahligen Adele.
Anwendungen
- Sei
eine Primzahl und
der Körper mit
Elementen. Da jede algebraische Erweiterung
von
zyklisch ist vom Grade
die Galois-Gruppe also isomorph zu
ist
, wobei
den algebraische Abschluss von
bedeutet. Dabei entspricht der Frobeniusautomorphismus
-
- dem Erzeuger
von
[30]
der Endomorphismenring des Moduls
- In additiven Gruppen können proendliche Vielfachheiten definiert werden, in multiplikativen proendliche Exponenten.
- Die Fibonacci-Zahlen können für proendliche Indizes definiert werden.[31]
Siehe auch
Literatur
- Michael D. Fried, Moše Yardēn: Field arithmetic. 3rd. 2008
- Hendrik Lenstra: Profinite Groups. (PDF)
- James Milne: Class Field Theory. (PDF)
- Paul Fjelstad: The repeating integer paradox. In: The College Mathematics Journal. Band 26, Nr. 1, Januar 1995, S. 11–15, doi:10.2307/2687285.
- Philippe Gille, Tamás Szamuely: Central Simple Algebras and Galois Cohomology. (PDF) doi:10.2277/0521861039
Weblinks
- Jon Brugger: Pro-endliche Gruppen. (PDF)
- Jakob Stix: Proendliche Gruppen (Vorlesung im Sommersemester 2016 an der Uni Frankfurt)
- Hendrik Lenstra: Profinite number theory. (PDF)
- Hendrik Lenstra: Profinite Fibonacci numbers. (PDF)
Einzelnachweise und Anmerkungen
- ↑ In #Fried S. 14 Prüfer group (deutsch: Prüfergruppe) genannt. (S.a. Teilbare Gruppe)
- ↑
#Gille
3. Die proendliche Vervollständigung von
- ↑ Beweis im Artikel Limes (Kategorientheorie)
- ↑
Trotzdem gibt es keine mit den Ringoperationen
verträgliche Anordnung
von
: Die proendlichen Zahlen können also nicht angeordnet werden. (Das gilt auch schon für die p-adischen Zahlen.)
- ↑
Im Abschnitt Pseudometrik#Definition
einer Spanne durch eine uniforme Struktur wird ausgehend von einer
uniformen Struktur, hier
unter Zuhilfenahme der Abzählbarkeit des Fundamentalsystems eine Pseudometrik konstruiert, die ihrerseits wieder
induziert.
Es gibt jedoch sogar eine Metrik, die die uniforme Strukturinduziert:
- Sei dazu
für ,
sonst. - der „!-Wert“ eines
. [
misst die Nähe zur Null (den Grad der Teilbarkeit) von
durch Teiler der Form
(gesprochen: enn Fakultät) – in Analogie zum
-Wert in den Ringen
der den maximalen Exponenten
bei der Teilbarkeit durch
angibt, oder auch zu
(s. Lenstra Profinite number theory. S. 21) in den archimedischen Systemen.]
- Dann gilt für
mit
- mit passenden
und
woraus
Der symmetrische Fall
führt zu
Beide Fälle zusammen ergeben
- Die damit gebildete Abstandsfunktion
- erfüllt die Forderungen für eine Metrik und ist eine Ultrametrik:
(1) Positive Definitheit: und
(2) Symmetrie: (3) Verschärfte Dreiecksungleichung: Diese Metrik ist wie die uniforme Struktur im Text durch den Grad der Teilbarkeit definiert, so dass sie als uniforme Strukturen übereinstimmen.
NB: Die Folge
ist kofinal in
. Und jede monotone kofinale Folge definiert eine Metrik mit derselben uniformen Struktur.
- ↑
Denn es ist
- ↑
Diese Nullnetze
sind genau die monotonen in
kofinalen Netze, denn
- ↑ #Brugger Satz 7.2.
- ↑ s. Artikel Limes (Kategorientheorie)
- ↑ Eine Implementierung dazu ist der #Algorithmus mit dem System A003418 der kleinsten gemeinsamen Vielfachen.
- ↑ a
b
Der hier vorkommende Ordnungstyp
ist nicht
sondern der in zwei Dimensionen (der Folge der Primzahlen und der Folge der Exponenten) unendliche Ordnungstyp
mit
für fast alle
geht komponentenweise
- ↑ Lenstra Profinite number theory. S. 17
- ↑ vorausgesetzt, zu jeder Primzahlpotenz gibt es unter den Stellenwerten ein Vielfaches,
- ↑ Wie bei allen Stellenwertnotationen üblich, b-adischen wie p-adischen, notiert man die kleinen Exponenten auf der rechten Seite der Zeile. Dort starten auch die meisten Algorithmen, insbesondere Addition und Multiplikation. Die p-adischen und die proendlichen Zahlen setzen sich nach links hin zu den höheren Exponenten potentiell bis ins Unendliche fort.
- ↑ Im Unterschied zu den Notationen mit gleichbleibender Basis wechseln die Basen von Stelle zu Stelle, hängen aber von nichts als der Nummer der Stelle ab. Wenn sie mitnotiert werden, sind sie so fix wie eine Skalenteilung an einer Koordinatenachse.
- ↑ Dies ist in Einklang mit der Konvention bei fakultätsbasierten Zahlensystemen (so auch bei Lenstra Profinite Groups Example 2.2).
- ↑
- ↑
- ↑
a
b
Diese Folge ist streng monoton kofinal
in
- ↑ Werden die Basen (oder Moduln) mitnotiert, dann sind damit auch die Restklassen angegeben, auf die sich die Zwischensummen beziehen. Dies gilt auch für Notationen, bei denen die Basen anderweitig bekannt gemacht sind oder erschlossen werden können.
- ↑
 mathworld.wolfram.com Eric W. Weisstein „Kleinstes
gemeinsames Vielfaches.“ From MathWorld--A Wolfram Web Resource
mathworld.wolfram.com Eric W. Weisstein „Kleinstes
gemeinsames Vielfaches.“ From MathWorld--A Wolfram Web Resource - ↑
Diese Folge ist monoton kofinal
in
- ↑ Lenstra Profinite Groups Example 2.1
- ↑
Die Schreibweise
wird vermieden, um nicht die Assoziation eines Körpers hervorzurufen.
- ↑ Fjelstad S. 11.
- ↑
Es gilt jedoch
- ↑ Die Stellenwerte (oder Moduln) sind die Gewichte, mit denen die Ziffern zu multiplizieren sind, z.B. die Ziffer 3 mit dem akkumulierten Gewicht 12 = 2·3·2·1.
- ↑
Betrachtet man also diese Reihe als ganzzahlige
Zahlenfolge im Ring
so ist sie gleich (konvergiert sie gegen die dortige) 1. Man kann sie auch als Folge in
auffassen, dann konvergiert sie gegen (die dortige) 0.
- ↑ Lenstra Profinite number theory. S. 7
- ↑ Milne, Ch. I Example A. 5.
- ↑ Lenstra Profinite Fibonacci numbers. S. 299


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 15.03. 2023