
Rheologisches Modell
Rheologische Modelle beschreiben in der Rheologie, der Wissenschaft vom Fließ- und Deformationsverhalten der Materialien, den Zusammenhang zwischen der Verformung eines Körpers und der diese Verformung bewirkenden äußeren Spannung. Da verschiedene Materialien ein erheblich voneinander abweichendes Verhalten zeigen, sind unterschiedliche Modellkörper notwendig. Dazu werden die drei idealisierten Grundeigenschaften Elastizität, Viskosität und Plastizität mit den der Mechanik entlehnten Grundmodellkörpern Feder, Dämpfungszylinder und Reibklotz beschrieben. Komplexeres, der Realität näher kommendes Verhalten kann dann durch Reihen- und Parallelschaltung mehrerer dieser idealisierten Grundelemente modelliert werden, analog zu idealen und realen elektrischen Bauelementen.
Das Verhalten der Grundelemente lässt sich mathematisch mit einfachen
Gleichungen abbilden, die den Zusammenhang zwischen Deformation
und Spannung
darstellen. Die Deformation kann dabei als Dehnung,
Stauchung, Scherung oder Torsion
erfolgen. Aus diesen Grundgleichungen können Gleichungen für das Verhalten der
zusammengesetzten Modellkörper hergeleitet werden.
Die Modelle erlauben es damit, unterschiedliches Fließ- und Deformationsverhalten qualitativ und quantitativ zu beschreiben, zu kategorisieren und vorherzusagen. Sie finden damit außer in der Rheologie selbst in vielen Bereichen der Technik und Naturwissenschaft Anwendung, z.B. in der Werkstoffwissenschaft, in der Geologie und in der Lebensmitteltechnik.
Da sie nur Aussagen über das makroskopische Verhalten von Materialien ermöglichen, nicht aber über die Ursachen dafür, die in der jeweiligen Stoffstruktur liegen, zählen sie zur phänomenologischen Rheologie. Die Modellkörper wurden zum Großteil Ende des 19. bis Mitte des 20. Jahrhunderts von ihren jeweiligen Namensgebern entwickelt.
Rheologische Phänomene

Die Notwendigkeit verschiedener Modelle zeigt sich, wenn man sich das unterschiedliche Deformationsverhalten von Materialien vor Augen führt: Lässt man beispielsweise eine Gummikugel auf eine Oberfläche fallen, verformt sie sich beim Aufprall und springt zurück, nimmt also ihre ursprüngliche Form wieder ein (elastisches Verhalten). Ein Wassertropfen dagegen verläuft nach dem Aufprall unter dem Einfluss der Schwerkraft, deformiert sich also dauerhaft (viskoses Verhalten). Eine Kugel aus Knetmasse bildet beim Aufprall eine Art Halbkugel, verformt sich also dauerhaft, ohne jedoch völlig zu zerfließen (plastisches Verhalten). Sogenannter Hüpfender Kitt aus Silikonkautschuk springt dagegen bei einem schnellen Aufprall wie eine Gummikugel zurück, zerfließt aber bei einem langsamen Aufprall allmählich wie ein Flüssigkeitstropfen, zeigt also eine Kombination verschiedener Verhaltensweisen (sogenanntes viskoelastisches Verhalten).
In der Realität zeigen aber praktisch alle Materialien elastisches, viskoses und plastisches Verhalten gleichzeitig, lediglich die Ausprägung und die Art des Zusammenwirkens der einzelnen Eigenschaften unterscheiden sich. Würde man die Gummikugel beispielsweise über ein Jahr einspannen, so nähme auch sie nach einer Entspannung ihre ursprüngliche Form nicht mehr vollständig ein, sondern würde eine bleibende Deformation aufweisen. Sie zeigt also kein ideal elastisches Verhalten. Auch scheinbar eindeutig starre Materialien wie ausgehärteter Beton oder Gestein kriechen, d.h. sie fließen über lange Zeiträume allmählich weg.
Die drei Grundmodelle
Ideale Elastizität
Ein ideal elastischer Körper ist durch folgende Eigenschaften gekennzeichnet:
- Er reagiert auf eine einwirkende Spannung
mit einer sofortigen Deformation
ohne zeitliche Verzögerung.
- Das Ausmaß der Deformation ist begrenzt und proportional zur Spannung.
- Wirkt die Spannung nicht mehr ein, bewegt sich der Körper ohne Verzögerung in seine Ausgangslage zurück, die Verformung ist also reversibel.
- Es gilt das Hookesche
Gesetz
. Die Konstante
ist hierbei der Elastizitätsmodul bei Dehnung, der Kompressionsmodul bei Stauchung oder der Schubmodul bei Scherung oder Torsion.
Dies sind die Eigenschaften eines idealen Festkörpers und können durch eine Feder, das sogenannte Hooke-Element, modelliert werden.
Ideale Viskosität
Ein ideal viskoser Körper zeigt diese charakteristischen Eigenschaften:
- Er reagiert auf eine einwirkende Spannung
mit einer zeitlich verzögerten Deformation
.
- Das Ausmaß der Deformation ist unbegrenzt solange die Spannung einwirkt.
- Wirkt die Spannung nicht mehr ein, bleibt die Deformation bestehen, die Verformung ist also irreversibel.
- Die Deformationsgeschwindigkeit ist proportional zur einwirkenden
Spannung. Es gilt
. Die Konstante
ist hierbei die dynamische Viskosität, die meist in Scherung, aber auch in Dehnung (Dehnviskosität) betrachtet wird.
Damit ist eine ideale Flüssigkeit, auch Newtonsches Fluid genannt, beschrieben. Sie kann durch einen flüssigkeitsgefüllten Dämpfungszylinder mit einem Kolben darin, ähnlich einem Stoßdämpfer, modelliert werden. Der Dämpfungszylinder wird als so groß angenommen, dass der Kolben nicht an die Grenze seiner Beweglichkeit gelangt. Dieses Modell heißt Newton-Element.
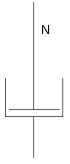
Ideale Plastizität
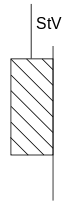
Ein ideal plastischer Körper verhält sich folgendermaßen:
- Solange die Spannung
unterhalb der Fließgrenze
liegt, erfolgt keine Deformation.
- Wird die Fließgrenze überschritten, verformt sich der Körper irreversibel mit nicht definierter Geschwindigkeit.
- Es gilt also
Damit verhält sich ein ideal plastischer Körper unterhalb der Fließgrenze wie ein ideal starrer Festkörper, oberhalb der Fließgrenze wie eine Flüssigkeit mit unendlich kleiner Viskosität. Dieses nichtlineare Verhalten lässt sich durch einen Klotz, der sich auf einer reibungsbehafteten Oberfläche befindet, modellieren. Auch dieser lässt sich erst nach Überschreiten der Haftreibungskraft in Bewegung versetzen. So ein Modellkörper wird als St.-Venant-Element bezeichnet.
Zusammengesetzte Modellkörper
Reihen- und Parallelschaltung
Aus den Grundmodellen können nun komplexere, eher der Realität entsprechende
Modelle aufgebaut werden. Schaltet man
Modellkörper in Reihe, also hintereinander, so erfahren alle dieselbe
Spannung:
Die Dehnung des Gesamtkörpers ist die Summe der Dehnungen der Einzelkörper:
Bei Parallelschaltung sind die Verhältnisse genau umgekehrt. Die Körper erfahren dieselbe Dehnung, die Spannungen addieren sich:
Elastoplastizität
 |
 | |
|
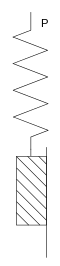
Prandtl-Körper |
Erweiterung mit parallel
geschaltetem
Hooke-Element |
Viele Feststoffe wie z.B. Stahl zeigen bis zum Erreichen einer Streckgrenze elastisches Verhalten, oberhalb der Streckgrenze setzt eine bleibende plastische Verformung ein. Dieses Verhalten kann durch die Reihenschaltung eines Hooke-Elementes mit einem St.-Venant-Element modelliert werden, was den Prandtl-Körper ergibt. Wegen der Reihenschaltung gilt:
Bis zum Erreichen von
gilt
,
es wirkt sich also nur das Hooke-Element aus. Erreicht die Spannung die
Fließgrenze, setzt die plastische Verformung ein und die Spannung steigt nicht
mehr weiter an.
Aber auch dieses Verhalten stellt noch eine Idealisierung dar. Bei realen Materialien ist die plastische Verformung nicht unbegrenzt, sondern wird durch Verfestigungsvorgänge beschränkt. Dies kann durch Parallelschaltung eines weiteren Hooke-Elementes berücksichtigt werden.
Für
hat das plastische Element keinen Einfluss, es liegt eine Parallelschaltung
zweier elastischer Elemente vor, die sich wie ein einziges Hooke-Element
verhalten:
Für
setzt die plastische Verformung ein. Die Spannung im Strang mit dem
St.-Venant-Element steigt nun nicht weiter an und beträgt konstant
.
Damit gilt:
Nach
aufgelöst ergibt sich:
Auch nach Überschreiten der Streckgrenze, weist dieses Modell also ein
prinzipiell elastisches Verhalten auf, allerdings mit verändertem E-Modul und um
reduzierter Spannung.
Viskoelastizität
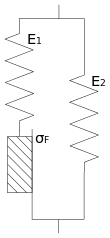
Ein viskoelastischer Körper weist gleichzeitig viskoses und elastisches Verhalten auf. Dies entspricht der Kombination eines Hooke- mit einem Newton-Element. Dieser Effekt tritt häufig bei Polymeren und ihren Schmelzen auf.
Beim Kelvin-Körper,
auch als Kelvin-Voigt-Körper
bezeichnet, werden die beiden Elemente parallel geschaltet. Wird eine äußere
Spannung
aufgebracht und beibehalten (Kriechversuch),
so verformt sich die Feder elastisch, wird dabei aber durch das
Newton-Element gebremst, so dass die Verformung zeitlich verzögert
eintritt. Mit der Zeit nähert sich die Verformung dem Wert an, der durch das
Hooke-Element vorgegeben ist. Verschwindet die äußere Kraft, so federt
der Körper allmählich in die Ausgangslage zurück. Die Verformung des
Kelvin-Körpers ist damit begrenzt und reversibel, kennzeichnet also das
Verhalten eines Festkörpers.
Das Verhalten des Kelvin-Körpers lässt sich mathematisch durch die Differentialgleichung
beschreiben. Mit der Randbedingung
ergibt sich für eine aufgebrachte Spannung
die Lösung
Für
gilt
,
die Verformung nähert sich also dem Wert des reinen elastischen Elementes
an.
Oskar Emil Meyer beschrieb das Modell erstmals 1874, wegen späteren Arbeiten von William Thomson (Lord Kelvin) und Woldemar Voigt wird es aber Kelvin-(Voigt-)Modell genannt.
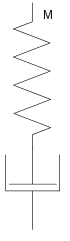
Der Maxwell-Körper, die Reihenschaltung von Hooke- und Newton-Element, stellt eine viskoelastische Flüssigkeit dar. Die Verformung ist hier aufgrund des Dämpfungszylinders unbegrenzt und irreversibel. Das rein viskose Verhalten wird hier um eine elastische Komponente ergänzt, die sich lediglich unmittelbar bei Be- und Entlastung bemerkbar macht: Die Feder spannt bzw. entspannt sich sofort, während das viskose Element Zeit braucht, um sich zu verformen. Wird das Material bis zu einem gewissen Punkt deformiert und diese Verformung dann beibehalten (Relaxationsversuch), so verschwindet mit der Zeit die Spannung, da sich die Feder entspannt und deren Deformation durch das viskose Element aufgenommen wird.
Wegen der Reihenschaltung gilt
Mit
und
ergibt sich
Beidseitige Ableitung ergibt die Differentialgleichung
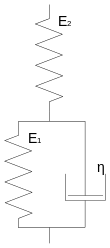
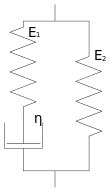
Durch Hinzufügen weiterer Elemente lassen sich komplexere Verhaltensweisen darstellen. Der Zenerk- bzw. der Zenerm-Körper besteht aus der Reihenschaltung eines Kelvin-Körpers mit einem Hooke-Körper bzw. der Parallelschaltung eines Maxwell-Körpers mit einem Hooke-Element. Sie beschreiben beide ein Festkörperverhalten und haben gegenüber dem Kelvin-Körper den Vorteil, dass sie bei beliebig hoher Dehngeschwindigkeit nicht eine unrealistische, unendlich hohe Spannungsspitze aufweisen.
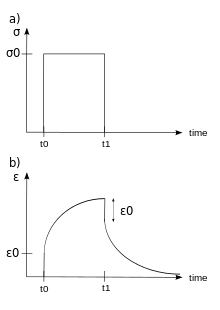
Auf eine plötzliche Belastung
reagiert der Zenerk-Körper wegen der in Reihe geschalteten
Feder
mit einer spontanen Verformung
.
Danach zeigt er das viskoelastische Verhalten des Kelvin-Elementes. Bei
Entlastung entspannt er sich ebenfalls schlagartig um
,
um dann langsam in seine Ausgangsposition zurückzukehren. Ein
Zenerm-Körper verhält sich im Kriechversuch qualitativ gleich.
Es ist auch möglich dem Zenerm-Modell weitere parallele Maxwell-Körper mit
unterschiedlichen Moduli und Viskositäten hinzuzufügen. Dieses erweiterte
Viskoelastizitätsmodell erlaubt, das Abklingverhalten exakter an Messwerte
anzupassen.
| Zenerk | Zenerm |
|---|---|
 |
 |
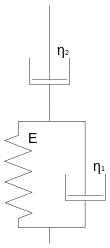
Beim Lethersich- und Jeffreys-Modell wird jeweils anstelle eines Hooke- ein Newton-Element hinzugefügt. Damit stellen die beiden Körper das Verhalten von Flüssigkeiten dar. Sie unterscheiden sich vom Maxwell-Körper dadurch, dass die reversible Verformung nicht spontan eintritt, sondern durch den hinzugefügten parallelen Dämpfungszylinder verzögert wird.
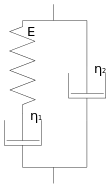
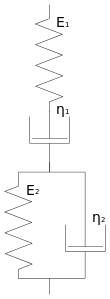
Das Burgers-Modell wurde 1935 zur Modellierung des Verhaltens von Asphalt und Bitumen vorgeschlagen. Es besteht aus der Reihenschaltung eines Maxwell- und Kelvin-Körpers. Auch Polymere können mit dem Burgers-Modell beschrieben werden. Diese weisen oft eine reversible Entropie-Elastizität, die von verdrillten Polymerknäulen, welche gerade gezogen werden, herrührt, und eine irreversible Verformung durch Aufbrechen von bzw. Versetzungen in molekularen Bindungen auf. Erstere wird durch den Kelvin-Körper, letztere durch den Maxwell-Körper verkörpert.
| Lethersich | Jeffreys | Burgers |
|---|---|---|
 |
 |
 |
Visko-(Elasto-)Plastizität
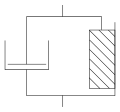
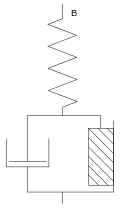
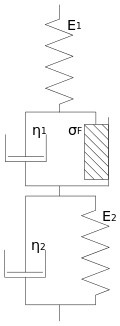
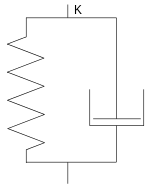
Die Kombination aus viskosem und plastischem Verhalten, also eine Flüssigkeit, die erst nach Überschreiten einer Grenzspannung fließt, findet sich bei sogenannten Bingham-Fluiden. So eine Viskoplastizität lässt sich idealisiert durch Parallelschaltung eines St.-Venant-Körpers mit einem Newton-Element darstellen. Dies wird als Bingham-Körper bezeichnet.
Allerdings verhalten sich Bingham-Fluide wie Ketchup oder Zahnpasta vor Erreichen der Fließgrenze nicht wie ein starrer Festkörper, wie es nach dem idealen Bingham-Modell der Fall wäre, sondern lassen sich bereits elastisch verformen. Dies lässt sich durch Vorschalten einer Feder darstellen, man erhält das Bingham-Hooke-Modell. Nach Überschreiten der Fließgrenze verhält sich dieser Körper wie eine viskoelastische Flüssigkeit. Es gilt also:
Dieses Modell vereinigt somit alle drei Grundeigenschaften in sich, zeigt also eine Visko-Elasto-Plastizität. In der Literatur wird solches Verhalten oft aber auch nur als Viskoplastizität bezeichnet.
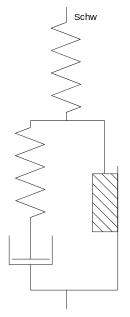
Untersuchungen an konzentrierter Gelatinelösung führten zur 1890 zur Entwicklung des Schwedoff-Körpers (siehe Einleitung). Dessen Verhalten ähnelt qualitativ dem des Bingham-Hooke-Modells.
Der Schofield-Scott-Blair-Körper stellt ein sehr umfangreiches Modell dar, aus dem alle bisherigen Körper abgeleitet werden können, wenn die entsprechenden Viskositäten zu unendlich, bzw. die entsprechenden Moduln zu 0 gesetzt werden.
Abweichungen der Modelle vom realen Verhalten
Das so modellierte Verhalten zeigt aber immer noch Unterschiede zum Verhalten
realer Materialien, auch bei komplexen Modellkörpern. Dies hat mehrere Gründe.
Das Hooke- und das Newton-Element gehen von einem linearen
Zusammenhang zwischen Spannung
und Deformation
,
bzw. Deformationsgeschwindigkeit
aus. In der Realität liegt aber häufig ein nichtlinearer
Zusammenhang vor. Insbesondere bei sogenannten nichtnewtonische
Fluiden treten Effekte wie Dilatanz
und Strukturviskosität
auf, d.h. die Viskosität ist keine Konstante mehr, sondern hängt wiederum
von der Deformationsgeschwindigkeit ab. Die Viskosität kann sich sogar bei
gleichbleibender Deformationsgeschwindigkeit mit der Zeit ändern, was als Thixotropie
bzw. Rheopexie bezeichnet wird.
Schließlich hängt das Deformationsverhalten auch von äußeren Einflüssen, vor
allem der Temperatur, ab.
Die Modellkörper können aber auch daran angepasst werden, indem man mathematisch die linearen Zusammenhänge durch nichtlineare Zusammenhänge ersetzt. So kann man nichtlineares Fließen durch den Eyring-Ansatz
anstelle des linearen Ansatzes
beschreiben. Dieser berücksichtigt sowohl die Temperatur
,
als auch die beiden Materialparameter
und
.
Der Faktor
ist die Boltzmann-Konstante.
Eine mathematisch simple und messtechnisch leicht umzusetzende Vorgehensweise zur exakteren Charakterisierung viskoelastischer Stoffe besteht darin, von einer sinusförmig oszillierenden Deformation auszugehen (Schwingungsrheometrie). Der viskose Anteil wird dabei durch den sogenannten Verlustmodul, der elastische durch den Speichermodul repräsentiert. Beide Größen können frequenz- und amplitudenabhängig gewählt werden. Dabei ist aber immer noch ein zumindest näherungsweise lineares Materialverhalten Voraussetzung.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 15.11. 2023