
Drallsatz

Der Drallsatz, Momentensatz, Drehimpulssatz, Impulsmomentsatz oder die Drehimpulsbilanz ist in der klassischen Mechanik ein physikalisches Gesetz, das besagt, dass zur Änderung des Drehimpulses eines Körpers ein Drehmoment an ihm aufgebracht werden muss. Ein Anwendungsbeispiel ist das Spielplatzkarussell im Bild. Um dies in Drehung zu versetzen, muss man es anstoßen. Technisch gesehen bringt man dabei ein Moment auf, das dem Karussell Drehimpuls zuführt. Die Drehimpulserhaltung sorgt dann dafür, dass das Karussell eine Weile weiter dreht. Reibungsmomente im Lager und Luftwiderstand erzeugen jedoch ein Gegenmoment, das den Drehimpuls aufzehrt und die Rotation schließlich wieder zum Erliegen bringt.
Die mathematische Formulierung des Drallsatzes lautet:
Darin ist
das von außen angreifende Moment,
der Drehimpuls des Körpers und
seine zeitliche Änderung, jeweils bezogen auf einen festen Punkt
,
für den häufig der Ursprung in einem Inertialsystem
benutzt wird. Deshalb wird der Index c im Weiteren nicht mehr explizit
angegeben. Im Spezialfall, wo die äußeren Momente verschwinden, zeigt sich, dass
der Drehimpuls erhalten bleibt. Entsprechend steht Drehimpulssatz auch
für den Drehimpuls-Erhaltungssatz.
Des Weiteren steht Momentensatz auch für den Momentensatz aus der
Statik. Die der Drehimpulsänderung entgegengesetzte d'Alembertsche
Trägheitskraft macht sich als Kreiselwirkung
bemerkbar.
Aus dem Drallsatz folgt das Prinzip von der Gleichheit der zugeordneten Schubspannungen oder die Symmetrie des (Cauchy’schen) Spannungstensors. Dieselbe Konsequenz hat auch das Boltzmann-Axiom, demgemäß innere Kräfte in einem Kontinuum momentenfrei sind. Somit sind der Drallsatz, die Symmetrie des Spannungstensors und das Boltzmann-Axiom in der Kontinuumsmechanik verwandte Begriffe.
Insbesondere in der Kreiseltheorie spielt der Drallsatz eine zentrale Rolle. In der Kontinuumsmechanik dient er dazu, den schiefsymmetrischen Anteil des Spannungstensors eindeutig zu bestimmen.
Der Drallsatz ist neben den Newton’schen Gesetzen ein fundamentales und unabhängiges Prinzip und wurde als solches erstmals von Leonhard Euler 1775 vorgestellt.
Geschichte
Jakob I Bernoulli wendete 1703 den Drallsatz an – ohne ihn jedoch explizit zu formulieren – um das Oszillationszentrum eines Pendels zu finden, was er bereits auch in einem ersten, etwas unrichtigen Versuch 1686 tat. Clifford Truesdell vermutete daher, dass der Drallsatz, als unabhängiges Gesetz der Mechanik und als kinetische Verallgemeinerung des statischen Gleichgewichtsprinzips der Drehmomente, als erstes von Jakob I Bernoulli 1686 benutzt wurde. Der Drallsatz ginge damit den Newton’schen Gesetzen von 1687 voraus.
Leonhard Euler benutzte in einem Werk von 1744 als erster die Prinzipe des Impulses und des Drehimpulses, um die Bewegungsgleichungen eines Systems aufzustellen. Im Jahr 1750 veröffentlichte er in der Abhandlung „Entdeckung eines neuen Prinzips der Mechanik“ die Kreiselgleichungen, die heute aus dem Drallsatz hergeleitet werden, die Euler jedoch für den starren Körper aus dem zweiten Newton’schen Gesetz folgern konnte. Erst im Jahr 1775, nach Studien über ebene elastische Kontinua, für die die Bilanz der Momente unentbehrlich ist, erhob Euler den Drallsatz zu einem eigenständigen Prinzip zur Berechnung der Bewegungen von Körpern.
Augustin-Louis
Cauchy führte 1822 den Spannungstensor ein, dessen Symmetrie in
Kombination mit dem Impulssatz die Erfüllung des Drallsatzes im allgemeinen Fall
des deformierbaren Körpers sicherstellt. Die Interpretation
des Drallsatzes wurde erstmals von P. Saint-Guilhem 1851 erkannt.
Ludwig Boltzmann hat 1905 darauf hingewiesen, dass bei der Zerlegung eines Körpers in kleinere (infinitesimale) Volumenelemente die inneren Reaktionen alle statischen Gleichgewichtsbedingungen zu erfüllen haben. Georg Hamel prägte für diese Aussage den Namen Boltzmann-Axiom.
Kinetik der Rotation
Die Kinetik
beschäftigt sich mit Zuständen, die sich nicht im Gleichgewicht befinden. Nach
dem 2. Newtonschen
Gesetz führt eine resultierende äußere Kraft an einem Körper zu einer
Geschwindigkeitsänderung (Beschleunigung).
Analog dazu bedeutet ein resultierendes äußeres Drehmoment eine Änderung der Winkelgeschwindigkeit
resultierend in einer Winkelbeschleunigung
.
Das Trägheitsverhalten bezüglich der Rotation hängt nicht nur von der Masse
eines Körpers, sondern auch von deren räumlicher Verteilung ab.
Bei einem starren Körper wird dies durch das Trägheitsmoment Θ ausgedrückt. Bei einer Drehung um eine feste Achse gilt für das Drehmoment in Richtung dieser Achse:
Hierbei ist zu beachten, dass das Trägheitsmoment nicht nur von der Position der Drehachse (siehe Steinerscher Satz), sondern auch von ihrer Richtung abhängig ist. Soll die obige Gleichung allgemeiner für jede beliebige Raumrichtung formuliert werden, so muss stattdessen der Trägheitstensor Θ verwenden werden:
siehe unten. Das Rechenzeichen „ד bildet das Kreuzprodukt.
Im zweidimensionalen Spezialfall bewirkt ein Drehmoment lediglich eine Beschleunigung oder Abbremsung einer Rotationsbewegung. Im allgemeinen dreidimensionalen Fall kann es hingegen auch die Richtung der Rotationsachse verändern (siehe z.B.: Präzession).
Die vielfältigen Analogien in der Kinetik von Translation und Rotation sind bei Rotation angegeben.
Formulierungen
Drallsatz in der Punktmechanik
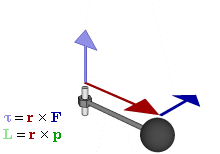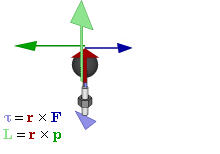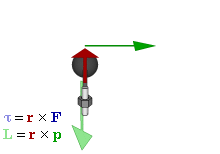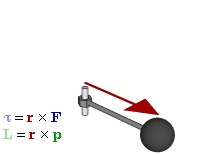
Der Zusammenhang zwischen Impulssatz und Drallsatz wird in der Punktmechanik deutlich.
Ein Körper
sei dazu durch n Massenpunkte
mk an den Orten
gegeben. An diesem gegen andere Massen abgegrenzten System, sind zwei Arten von
Kräften zu unterscheiden: Zum Einen gibt es die inneren Kräfte
,
die zwischen jeweils zwei zum System gehörenden Massenpunkten
mj und mk wirken und daher immer paarweise
entgegengesetzt auftreten, siehe Actio
und Reactio. Zum Anderen gibt es die äußeren Kräfte
,
die zwischen Systemmassen und einer sich außerhalb des Systems befindenden Masse
wirken und die daher am System nur einmal auftreten. Dann
lautet der Impulssatz für jeden einzelnen Massenpunkt
()
Der Drall des Körpers um den Ursprung ist die Summe der Drehimpulse der
Massenpunkte gemäß
und die zeitliche Ableitung davon ergibt sich zu
Die Beschleunigungen können mit dem Impulssatz durch die angreifenden Kräfte ausgedrückt werden:
weil die inneren Kräfte gemäß
immer paarweise entgegengesetzt an zwei wechselwirkenden Massenpunkten
mj und mk auftreten.
Massenpunkte lassen nur Zentralkräfte zu und Siméon Denis Poisson bewies 1833, dass ein System sich paarweise im Gleichgewicht haltender Zentralkräfte kein resultierendes Drehmoment ausüben, womit dann die unterstrichene Summe wegfällt. Mit dieser oft nicht genannten Voraussetzung entsteht der Drallsatz in der Punktmechanik
worin
das am System angreifende resultierende äußere Moment ist. Der Drallsatz
erscheint so in der Punktmechanik als Folgerung aus dem Impulssatz, was
allerdings das Resultat der Idealisierung der Massen als Massenpunkte ist, die nur Zentralkräfte
aufnehmen können.
Georg Hamel nannte die Punktmechanik „eine intellektuelle Unsauberkeit“ und meinte „was man unter Punktmechanik versteht, ist nichts anderes als der Schwerpunktsatz.“ Die Punktmechanik ist zur Herleitung des Drallsatzes völlig unzureichend. Bei der Übertragung dieser Überlegungen auf ein Kontinuum kommt die Annahme von Zentralkräften einem Axiom gleich, dem Boltzmann-Axiom unten, was zur Symmetrie des Cauchy’schen Spannungstensors führt.
Isaac Newton behauptete in seinen Principia nirgends, dass die Wechselwirkungskräfte Zentralkräfte seien. Wenn die Massen nicht durch Massenpunkte idealisiert werden, dann hilft der Drallsatz weiter: Nach ihm können die inneren Kräfte den Drehimpuls nicht verändern und somit muss die unterstrichene Summe der inneren Momente verschwinden. Natürlich gilt der Drallsatz auch in der Punktmechanik, aber er ist keine Folgerung aus Newtons zweitem Gesetz.
Drallsatz am Starren Körper
Beim starren Körper folgen die Massenpunkte der eulersche Geschwindigkeitsgleichung, was wichtige Konsequenzen hat und auf die Vektorgleichung
führt. Diese Gleichung wird gelegentlich Euler’sche
(Kreisel)gleichung genannt. Als Bezugspunkt für das Moment und den
Trägheitstensor eignen sich ein beliebiger unbeschleunigter Fixpunkt oder der
sich beliebig bewegende Massenmittelpunkt
des Körpers. Der erste Term auf der rechten Seite berücksichtigt die
Euler-Kräfte und der zweite die fiktiven Zentrifugalkräfte.
Würde der Starrkörper mit konstant gehaltener Winkelgeschwindigkeit
um die instantane Drehachse kreisen, dann würden die Zentrifugalkräfte ein
resultierendes Moment haben, das gerade
entspricht. Da bei der wirklichen Bewegung des starren Körpers die Drehachse
jedoch ihre Lage beständig ändert, hat Louis Poinsot für diese Zentrifugalkräfte den Namen fiktive
Zentrifugalkräfte vorgeschlagen.
| Beweis |
| Der Körper wird ähnlich wie oben als Vereinigung Der Starrkörper dreht sich mit der Winkelgeschwindigkeit Nach Newtons zweitem Gesetz „Kraft gleich Masse mal Beschleunigung“ ist Darin sind Dem Drallsatz zufolge sind die inneren Kräfte momentenfrei, siehe den vorausgehenden Abschnitt. Die Momente der an den einzelnen Massen angreifenden äußeren Kräfte Fi summieren sich dann zum resultierenden äußeren Moment Der erste Term Der zweite Term beinhaltet Euler-Kräfte summieren. Der unterstrichene Term ist der Trägheitstensor
Θ, der für den Starrkörper mit dem Einheitstensor
1 und dem dyadischen
Produkt „⊗“ von Vektoren gebildet wird. Das dyadische Produkt ist mit
drei beliebigen Vektoren Der dritte und letzte Term in obiger Momentengleichung bildet sich aus
den Zentrifugalkräften
ergibt. Die Kreiselwirkungen |
Diese Differentialgleichung
für die Winkelgeschwindigkeit
gilt als Vektorgleichung in jedem beliebigen Koordinatensystem, dessen Bewegung
genauestens bekannt ist, aber nur in einem körperfesten System sind die
Komponenten des Trägheitstensors immer zeitlich konstant. Bezüglich einer Orthonormalbasis
lauten die Komponentengleichungen:
Darin sind Θik die Komponenten des Trägheitstensors: Θii sind die Trägheitsmomente um die i-Achse und Θik mit k ≠ i die Deviationsmomente.
Ebene Bewegungen und Drehimpulssatz um den Momentanpol
Bei einer ebenen Bewegung, beispielsweise in der 1-2-Ebene, reduzieren sich die Komponentengleichung auf
wobei φ der Drehwinkel um die 3-Achse ist. Nach wie vor sind die Trägheitsmomente Θij (außer Θ33) in einem nicht körperfesten Bezugssystem im Allgemeinen von der Orientierung und damit vom Drehwinkel φ abhängig. Die letzten beiden Gleichungen dienen zumeist dazu, die Reaktionsmomente in 1- und 2-Richtung für den Zwanglauf in der 1-2-Ebene zu ermitteln. Wenn die 3-Richtung eine Hauptträgheitsachse ist, dann ergibt sich ohne solche Reaktionsmomente
Bei einer ebenen Starrkörperbewegung mit vorhandener Drehbewegung existiert
immer ein Momentanpol
genannter Raumpunkt ,
in dem erstens ein dort befindliches Partikel des Starrkörpers stillsteht und
sich zweitens die Bewegung als reine Drehbewegung um diesen Punkt darstellt.
Somit lautet das Geschwindigkeitsfeld
wenn
senkrecht zur Bewegungsebene ist. Bezüglich des Momentanpols hat der
Drehimpulssatz, wenn die 3-Richtung eine Hauptachse ist, eine ähnliche Form wie
bezüglich des Massenmittelpunkts:
wobei nun das Moment und das Massenträgheitsmoment bezüglich des Momentanpols berechnet wird.
| Beweis |
| Um das nachzuweisen, wird der Drehimpuls des starren Körpers als
Integral berechnet:
Der Vektor Der Trägheitstensor bezüglich des Momentanpols ist vom aktuell eingenommenen Raumgebiet Substantielle
Zeitableitung des Drehimpulses liefert mit Wenn der Momentanpol als Bezugspunkt gewählt wird |
Drallsatz am Kontinuum
Die in der Mechanik für ausgedehnte Körper formulierten physikalischen
Gesetze werden in der Kontinuumsmechanik als globale Integralgleichungen
ausgedrückt aus denen sich mit geeigneten Annahmen lokale Differentialgleichungen
ableiten lassen, die an jedem Punkt im Körper erfüllt sein müssen. Die äußeren
Kräfte und die von ihnen ausgeübten Momente werden wie in der Realität flächig
mit Spannungsvektoren
(mit der Dimension
Kraft pro Flächeninhalt) auf
der Oberfläche eingeleitet. Daneben gibt es noch volumenverteilte Kräfte
(mit der Dimension Kraft pro Masse)
wie beispielsweise die Gewichtskraft.
Dann lautet der Drallsatz in globaler Formulierung:
Darin ist ρ die Dichte
und
die Geschwindigkeit
am Ort
im Volumen
des Körpers, der die Oberfläche
besitzt. Das Integral auf der linken Seite steht für den Drehimpuls des Körpers
bezüglich eines beliebigen, zeitlich fixierten Bezugspunkts
und
bildet die zeitliche Änderung. Auf der rechten Seite stehen die Momente der
äußeren Kräfte. Das erste Integral bestimmt das Moment der volumenverteilten
Kräfte
und das zweite Integral das Moment der oberflächenverteilten Kräfte
.
Das Rechenzeichen
steht für das Kreuzprodukt.
Die äußeren Kräfte induzieren über
(
ist der nach außen gerichtete Normaleneinheitsvektor
auf der Oberfläche) und den Divergenzsatz
ein Spannungstensorfeld σ, das den ganzen Körper ausfüllt. Der Anteil an
den Integralen, der die Bahndrehimpulse
der Partikel betrifft, entfällt aufgrund der Impulsbilanz. Übrig bleibt ein
Momentenbeitrag, der von Schubspannungen zwischen den Partikeln verrichtet wird,
und damit dieser Beitrag verschwindet, muss der Cauchy'sche Spannungstensor
symmetrisch sein:
Bei Lagrange’scher
Betrachtungsweise betrifft das den zweiten-Piola-Kirchhoff-Spannungstensor
.
In Kombination mit der Impulsbilanz ist die Symmetrie des Spannungstensors
äquivalent zum Drallsatz.
Boltzmann-Axiom
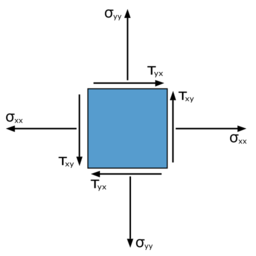
Ludwig Boltzmann hat 1905 darauf hingewiesen, dass bei der Zerlegung eines Körpers in (infinitesimal) kleine Volumenelemente jedes im statischen Gleichgewicht sein muss. An den Grenzflächen jedes Volumenelements müssen demnach die resultierenden inneren Kräfte und inneren Momente verschwinden. Das Cauchy’sche Fundamentaltheorem behandelt erstere Bedingung des Verschwindens der inneren Kräfte. Für die Forderung nach dem Verschwinden der inneren Momente prägte Georg Hamel den Namen Boltzmann-Axiom, da Boltzmann erstmals die Eigenständigkeit dieser Überlegung herausstellte. Das Boltzmann-Axiom ist für Starrkörper und viele deformierbare Körper zutreffend. Es gibt allerdings auch Kontinua, bei denen das Boltzmann-Axiom nicht anwendbar ist, siehe den folgenden Abschnitt.
Dieses Axiom ist äquivalent zur Symmetrie des Cauchy’schen Spannungstensors. Denn damit die Spannungsresultierenden am Volumenelement, blau im Bild, kein Moment ausüben, muss die Wirkungslinie der resultierenden Kraft durch die Mitte des Volumenelements gehen. Die Einzelkräfte ergeben sich aus den Spannungen multipliziert mit der Fläche auf der sie wirken. Die Wirkungslinie der Massenkräfte und der Kräfte der Normalspannungen σxx und σyy führen durch die Mitte des Volumenelements. Damit die Wirkungslinie der Schubspannungsresultierenden mit Komponenten τyx· dx in x-Richtung und τxy· dy in y-Richtung ebenfalls durch das Zentrum gehen, muss
gelten. Letzteres ist gerade die Aussage des Prinzips von der Gleichheit der zugeordneten Schubspannungen in der xy-Ebene.
Cosserat-Kontinuum
Neben dem momentenfreien klassischen Kontinuum mit symmetrischem
Spannungstensor, wurden auch Cosserat-Kontinua
definiert, die nicht momentenfrei sind (polare Kontinua).
Eine Anwendung eines solchen Kontinuums ist die Schalentheorie.
In den polaren Kontinua gibt es neben den Impulsflüssen
und -quellen
,
siehe oben, auch Drehimpulsflüsse und -quellen. Hier gilt das Boltzmann-Axiom
nicht und der Spannungstensor kann unsymmetrisch sein. Werden diese
Drehimpulsflüsse und -quellen wie in der Kontinuumsmechanik üblich behandelt,
entstehen Feldgleichungen, in denen der schiefsymmetrische Anteil des
Spannungstensors keine energetische Bedeutung hat. Der Drallsatz wird vom Energiesatz
unabhängig und dient der Bestimmung des schiefsymmetrischen Anteils des
Spannungstensors. Truesdell sah hierin den „wahren Grundsinn des
Drallsatzes“.
Flächensatz
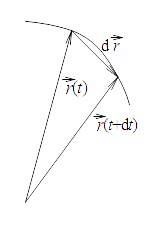
Der Flächensatz ist eine Folgerung aus dem Drallsatz in der Form: Das resultierende Moment ist gleich dem Produkt aus doppelter Masse und der Ableitung der Flächengeschwindigkeit.
Er bezieht sich auf den Fahrstrahl
zu einem Massenpunkt
mit Masse m. Dieser hat mit der Geschwindigkeit
und dem Impuls
den Drehimpuls
.
Der Fahrstrahl überstreicht in der (infinitesimalen) Zeit dt ein
Dreieck, dessen Inhalt
ist, siehe Bild und Kreuzprodukt
„ד. So ergibt sich
Mit dem Drallsatz wird daraus:
Der Spezialfall der ebenen, momentenfreien Bewegung in einem Zentralkraftfeld wird vom zweiten Kepler’schen Gesetz behandelt, das auch unter dem Namen Flächensatz bekannt ist.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 25.08. 2021